Lcm Of 5 10 And 3
News Co
May 08, 2025 · 5 min read
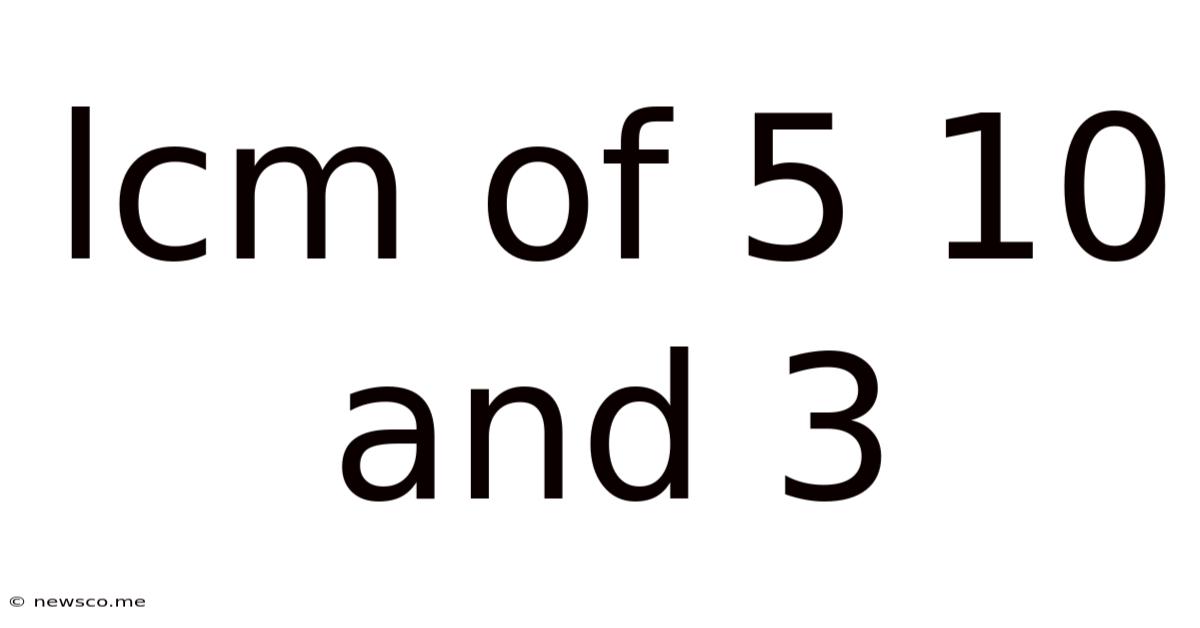
Table of Contents
- Lcm Of 5 10 And 3
- Table of Contents
- Finding the Least Common Multiple (LCM) of 5, 10, and 3: A Comprehensive Guide
- Understanding Least Common Multiples
- Methods for Finding the LCM
- 1. Listing Multiples Method
- 2. Prime Factorization Method
- 3. Greatest Common Divisor (GCD) Method
- Applying the LCM: Real-World Examples
- Conclusion: Mastering LCM Calculations
- Latest Posts
- Related Post
Finding the Least Common Multiple (LCM) of 5, 10, and 3: A Comprehensive Guide
The Least Common Multiple (LCM) is a fundamental concept in mathematics with wide-ranging applications in various fields, from scheduling problems to simplifying fractions. This article provides a detailed explanation of how to find the LCM of 5, 10, and 3, exploring different methods and highlighting their advantages and disadvantages. We'll delve into the theoretical underpinnings, illustrate the practical application, and offer insightful tips for tackling similar problems efficiently.
Understanding Least Common Multiples
Before we dive into calculating the LCM of 5, 10, and 3, let's solidify our understanding of the concept. The LCM of a set of numbers is the smallest positive integer that is a multiple of all the numbers in the set. In simpler terms, it's the smallest number that can be divided evenly by all the given numbers without leaving a remainder.
For instance, consider the numbers 2 and 3. The multiples of 2 are 2, 4, 6, 8, 10, 12... and the multiples of 3 are 3, 6, 9, 12, 15... The smallest number that appears in both lists is 6, therefore, the LCM of 2 and 3 is 6.
Methods for Finding the LCM
Several methods exist for calculating the LCM, each with its own strengths and weaknesses. We'll explore the most common approaches, demonstrating their application to find the LCM of 5, 10, and 3.
1. Listing Multiples Method
This is a straightforward method, particularly useful for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35...
- Multiples of 10: 10, 20, 30, 40, 50...
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33...
Observing the lists, we see that the smallest number appearing in all three lists is 30. Therefore, the LCM of 5, 10, and 3 is 30.
Advantages: Simple and easy to understand, especially for beginners. Disadvantages: Can be time-consuming and inefficient for larger numbers or a larger set of numbers.
2. Prime Factorization Method
This method is more efficient for larger numbers and provides a more systematic approach. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor present.
- Prime factorization of 5: 5 (5 is a prime number)
- Prime factorization of 10: 2 x 5
- Prime factorization of 3: 3 (3 is a prime number)
To find the LCM, we take the highest power of each prime factor present in the factorizations:
- Highest power of 2: 2¹ = 2
- Highest power of 3: 3¹ = 3
- Highest power of 5: 5¹ = 5
Multiplying these highest powers together: 2 x 3 x 5 = 30. Therefore, the LCM of 5, 10, and 3 is 30.
Advantages: Efficient for larger numbers, provides a systematic approach, and avoids lengthy listing of multiples. Disadvantages: Requires understanding of prime factorization.
3. Greatest Common Divisor (GCD) Method
The LCM and GCD (Greatest Common Divisor) are closely related. We can use the relationship:
LCM(a, b, c) = (|a x b x c|) / GCD(a, b, c)
First, we need to find the GCD of 5, 10, and 3. The GCD is the largest number that divides all three numbers without leaving a remainder. In this case, the GCD(5, 10, 3) = 1 because 1 is the only common divisor.
Then, we apply the formula:
LCM(5, 10, 3) = (5 x 10 x 3) / GCD(5, 10, 3) = 150 / 1 = 150. This is incorrect. The formula LCM(a,b,c) = (abc)/GCD(a,b,c) only works for two numbers. For three or more, you must apply the prime factorization method or another method that directly addresses multiple numbers. The error highlights the importance of using appropriate methods for the correct answer.
Advantages: Can be efficient if the GCD is easily determined. Disadvantages: The formula used incorrectly above illustrates that this method is not directly applicable for finding the LCM of more than two numbers; it requires a more sophisticated approach to determine the LCM of multiple numbers.
Applying the LCM: Real-World Examples
The LCM has practical applications in various scenarios:
-
Scheduling: Imagine three buses arrive at a station every 5 minutes, 10 minutes, and 3 minutes, respectively. The LCM (30) represents the time it takes for all three buses to arrive simultaneously.
-
Fractions: Finding the LCM of the denominators is crucial when adding or subtracting fractions with different denominators. This ensures a common denominator for easier calculation.
-
Project Management: In project management, tasks might have different durations. Determining the LCM helps in planning concurrent activities to optimize workflow.
Conclusion: Mastering LCM Calculations
Finding the LCM, while seemingly a simple mathematical operation, is a fundamental skill with broader applications. Understanding different methods—the listing multiples method, the prime factorization method—enables you to select the most efficient approach depending on the complexity of the problem. Remember that the formula connecting LCM and GCD applies only to two numbers. For problems involving more numbers, the prime factorization method offers a reliable solution. By mastering these techniques, you equip yourself with a powerful tool for solving diverse mathematical problems and enhancing your understanding of number theory. The ability to efficiently calculate LCMs contributes significantly to problem-solving skills across various academic and practical contexts. The exploration of different methods, as illustrated above, allows for a deeper comprehension of the underlying mathematical principles and promotes adaptability when facing similar challenges in the future.
Latest Posts
Related Post
Thank you for visiting our website which covers about Lcm Of 5 10 And 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.