Lcm Of 5 3 And 10
News Co
Apr 25, 2025 · 5 min read
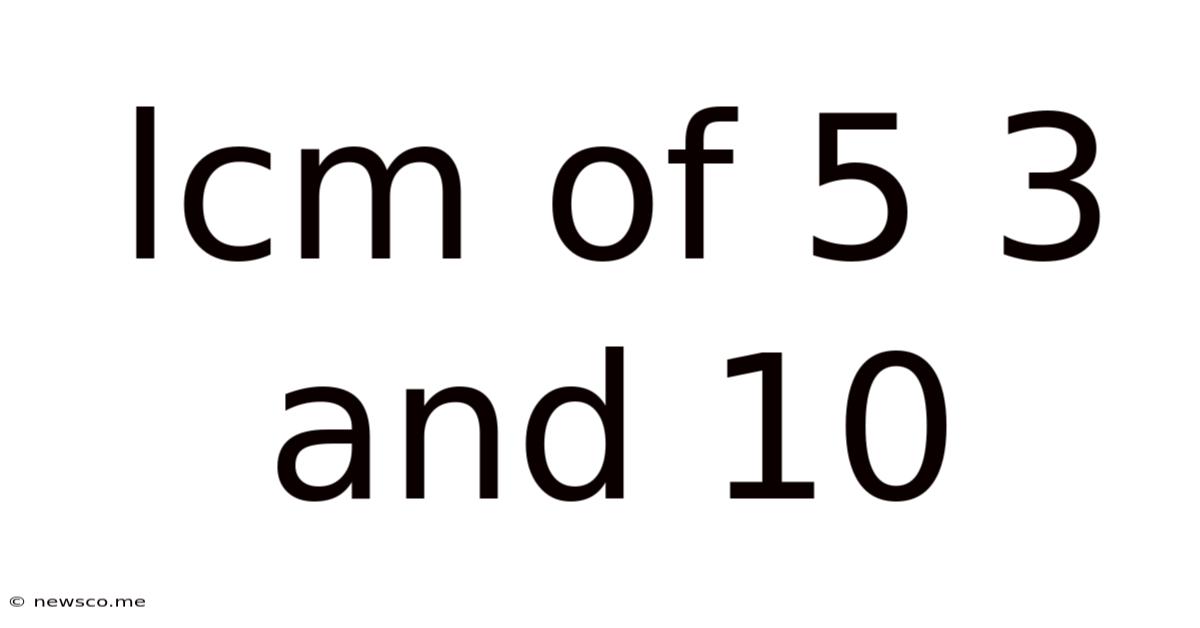
Table of Contents
Finding the LCM of 5, 3, and 10: A Comprehensive Guide
Finding the least common multiple (LCM) is a fundamental concept in mathematics, particularly crucial in areas like algebra, number theory, and even everyday problem-solving. This article delves deep into calculating the LCM of 5, 3, and 10, exploring multiple methods and providing a comprehensive understanding of the underlying principles. We'll also look at how this seemingly simple calculation can be applied to more complex scenarios.
Understanding Least Common Multiple (LCM)
Before we dive into calculating the LCM of 5, 3, and 10, let's establish a clear understanding of what the LCM actually represents. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers. This means that the LCM is a common multiple, and it's the least of all the common multiples. For example, the multiples of 5 are 5, 10, 15, 20, 25…; the multiples of 3 are 3, 6, 9, 12, 15…; and the multiples of 10 are 10, 20, 30, 40, 50…. The common multiples of 5, 3, and 10 include 30, 60, 90, and so on. The smallest of these is 30, making 30 the LCM of 5, 3, and 10.
Method 1: Listing Multiples
This is the most straightforward approach, especially for smaller numbers. We list out the multiples of each number until we find the smallest multiple that is common to all three.
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40…
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33…
- Multiples of 10: 10, 20, 30, 40, 50…
As you can see, the smallest common multiple is 30. Therefore, the LCM(5, 3, 10) = 30.
This method is simple and intuitive, but it can become cumbersome and inefficient when dealing with larger numbers or a greater number of integers.
Method 2: Prime Factorization
This method is more efficient and works well for larger numbers. It involves finding the prime factorization of each number and then building the LCM from the highest powers of each prime factor present.
- Prime factorization of 5: 5 = 5¹
- Prime factorization of 3: 3 = 3¹
- Prime factorization of 10: 10 = 2¹ × 5¹
To find the LCM, we take the highest power of each prime factor present in the factorizations:
- The highest power of 2 is 2¹ = 2
- The highest power of 3 is 3¹ = 3
- The highest power of 5 is 5¹ = 5
Now, multiply these highest powers together: 2 × 3 × 5 = 30. Therefore, the LCM(5, 3, 10) = 30.
This method is generally faster and more systematic than listing multiples, especially when dealing with larger numbers.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (Greatest Common Divisor) are closely related. There's a formula that connects them:
LCM(a, b) × GCD(a, b) = a × b
While this formula directly relates to two numbers, we can extend it to handle more than two by finding the LCM in stages.
First, let's find the GCD of 5 and 3. The GCD(5, 3) = 1 (as 5 and 3 share no common factors other than 1).
Now, let's use the formula to find the LCM of 5 and 3:
LCM(5, 3) × GCD(5, 3) = 5 × 3 LCM(5, 3) × 1 = 15 LCM(5, 3) = 15
Next, we find the LCM of 15 and 10. The GCD(15, 10) = 5. So,
LCM(15, 10) × GCD(15, 10) = 15 × 10 LCM(15, 10) × 5 = 150 LCM(15, 10) = 30
Therefore, the LCM(5, 3, 10) = 30.
This method demonstrates the elegant relationship between LCM and GCD, offering an alternative pathway to the solution.
Applications of LCM
The seemingly simple concept of LCM has far-reaching applications in various fields:
1. Scheduling and Time Management:
Imagine you have three tasks that repeat at different intervals: Task A repeats every 5 days, Task B every 3 days, and Task C every 10 days. To find when all three tasks will coincide, you need to find the LCM of 5, 3, and 10. The LCM, 30, indicates that all three tasks will coincide every 30 days.
2. Fraction Operations:
Finding a common denominator when adding or subtracting fractions requires finding the LCM of the denominators. For example, to add 1/5 + 1/3 + 1/10, we find the LCM of 5, 3, and 10, which is 30. Then we can rewrite the fractions with a common denominator of 30 before adding them.
3. Music Theory:
In music theory, the LCM is used to determine the least common multiple of the rhythmic values of notes in a musical piece, helping to understand the overall structure and rhythmic patterns.
4. Engineering and Design:
LCM plays a role in various engineering and design applications, especially in scenarios involving repetitive cycles or patterns. This could involve synchronizing machinery, designing gear ratios, or optimizing production processes.
5. Number Theory and Cryptography:
LCM is a fundamental concept in number theory and forms a building block in more advanced mathematical concepts used in cryptography and secure communication systems.
Conclusion: The Power of Simplicity
While finding the LCM of 5, 3, and 10 might seem like a trivial task, it illustrates a fundamental mathematical concept with significant practical applications. Mastering different methods for calculating LCM – from listing multiples to prime factorization and using the GCD – equips you with the tools to tackle more complex problems across various fields. Understanding LCM is not merely about solving mathematical problems; it’s about understanding the underlying structure and patterns within numbers, a skill valuable in diverse aspects of life and work. The seemingly simple calculation of LCM(5, 3, 10) = 30 opens the door to a world of mathematical exploration and practical applications.
Latest Posts
Related Post
Thank you for visiting our website which covers about Lcm Of 5 3 And 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.