Lcm Of 5 9 And 15
News Co
Apr 18, 2025 · 5 min read
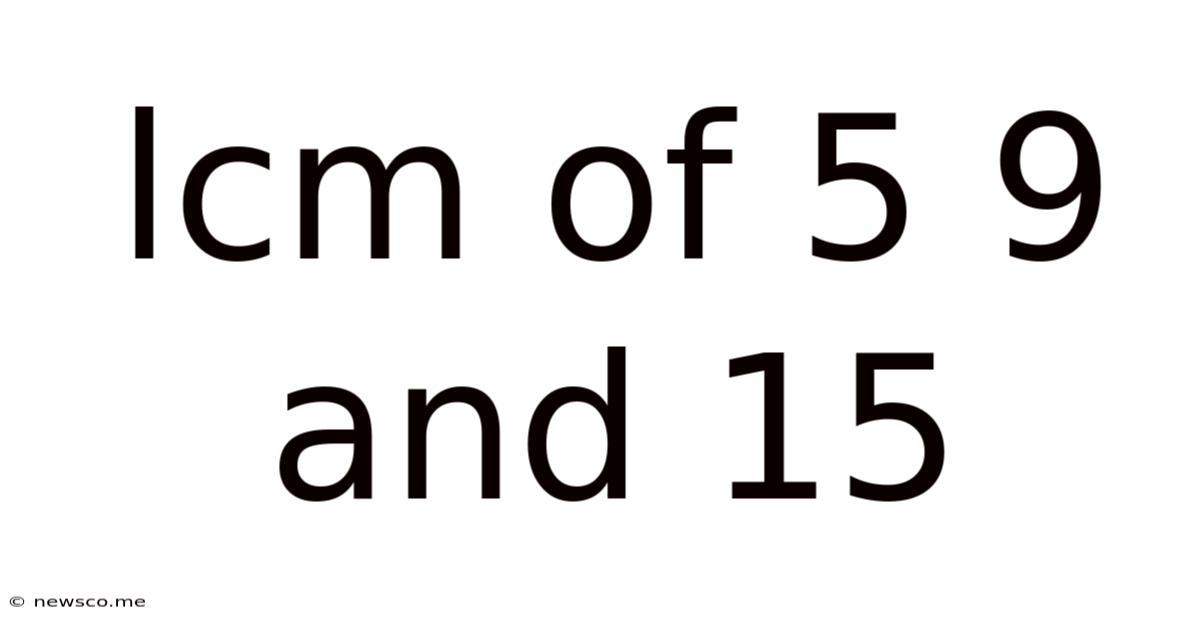
Table of Contents
Finding the LCM of 5, 9, and 15: A Comprehensive Guide
The least common multiple (LCM) is a fundamental concept in arithmetic and number theory. It represents the smallest positive integer that is a multiple of all the given integers. Understanding how to calculate the LCM is crucial for various mathematical operations, from simplifying fractions to solving problems in algebra and beyond. This article will delve into the methods of finding the LCM of 5, 9, and 15, exploring different approaches and highlighting their applications. We will also examine the broader significance of LCM in mathematics and its real-world applications.
Understanding the Least Common Multiple (LCM)
Before we jump into calculating the LCM of 5, 9, and 15, let's solidify our understanding of the concept. The LCM is the smallest number that is divisible by all the numbers in a given set. For instance, the LCM of 2 and 3 is 6 because 6 is the smallest positive integer divisible by both 2 and 3. It's distinct from the greatest common divisor (GCD), which is the largest number that divides all the numbers in a set.
Finding the LCM is particularly useful when dealing with fractions. When adding or subtracting fractions with different denominators, finding the LCM of the denominators allows us to find a common denominator, simplifying the calculation.
Methods for Calculating the LCM of 5, 9, and 15
Several methods exist for calculating the LCM, each with its advantages and disadvantages. Let's explore the most common ones in the context of finding the LCM of 5, 9, and 15:
1. Listing Multiples Method
This is the most straightforward method, especially for smaller numbers. We list the multiples of each number until we find the smallest multiple common to all three:
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50...
- Multiples of 9: 9, 18, 27, 36, 45, 54, 63...
- Multiples of 15: 15, 30, 45, 60, 75...
By comparing the lists, we observe that the smallest common multiple is 45. Therefore, the LCM of 5, 9, and 15 is 45. This method is simple but can become cumbersome when dealing with larger numbers.
2. Prime Factorization Method
This method leverages the fundamental theorem of arithmetic, which states that every integer greater than 1 can be uniquely represented as a product of prime numbers. The steps are as follows:
-
Find the prime factorization of each number:
- 5 = 5 (5 is a prime number)
- 9 = 3 x 3 = 3²
- 15 = 3 x 5
-
Identify the highest power of each prime factor present:
- The prime factors are 3 and 5.
- The highest power of 3 is 3² = 9.
- The highest power of 5 is 5¹ = 5.
-
Multiply the highest powers together:
- LCM(5, 9, 15) = 3² x 5 = 9 x 5 = 45
This method is more efficient than listing multiples, especially for larger numbers, as it avoids the need to list numerous multiples.
3. Greatest Common Divisor (GCD) Method
The LCM and GCD are related through the following formula:
LCM(a, b) x GCD(a, b) = a x b
This relationship holds true for any two numbers a and b. While it's less straightforward for three or more numbers, we can use it iteratively. First, we find the LCM of two numbers, and then we find the LCM of that result and the third number. To use this method effectively, we first need to find the GCD of our numbers:
Finding the GCD of 5, 9, and 15:
The GCD of 5 and 9 is 1 (they share no common factors other than 1). The GCD of 1 and 15 is 1. Therefore, the overall GCD of 5, 9, and 15 is 1.
However, this method is not as practical for finding the LCM of three or more numbers directly because the formula LCM(a, b, c) x GCD(a, b, c) = a x b x c doesn't hold true. It’s more efficient to use prime factorization in this case.
Applications of LCM
The LCM finds its application in diverse fields:
-
Fraction Arithmetic: As mentioned earlier, finding the LCM of denominators is essential for adding or subtracting fractions. For example, to add 1/5 and 1/9, we would find the LCM of 5 and 9 (which is 45), then convert the fractions to equivalent fractions with a denominator of 45 before adding.
-
Scheduling Problems: The LCM is frequently used to solve problems related to scheduling recurring events. Imagine two events happening at different intervals – one every 5 days and another every 9 days. The LCM will tell us when both events will occur on the same day again. In this case, LCM(5, 9) = 45, meaning both events will occur on the same day every 45 days.
-
Gear Ratios: In mechanics, the LCM is used in calculating gear ratios and determining the rotational speeds of interconnected gears.
-
Music Theory: Musical intervals and rhythmic patterns can be analyzed and understood using LCM. The LCM helps determine the least common period at which different rhythmic patterns repeat synchronously.
-
Construction and Engineering: The LCM plays a role in optimizing material usage and timing in construction projects.
Conclusion
Calculating the LCM of 5, 9, and 15 is a straightforward process, especially using the prime factorization method, which yields the result of 45. Understanding the concept of LCM and mastering its calculation is crucial in various areas of mathematics, science, and engineering. While the listing multiples method is useful for small numbers, prime factorization provides a far more efficient approach for larger numbers or more complex scenarios. The applications of LCM extend far beyond simple arithmetic, making it a fundamental concept worth understanding thoroughly. By grasping these methods and their applications, you equip yourself with a valuable tool for solving a wide range of problems. Remember to choose the method best suited to the problem's complexity for optimal efficiency.
Latest Posts
Related Post
Thank you for visiting our website which covers about Lcm Of 5 9 And 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.