Lcm Of 6 3 And 2
News Co
Apr 21, 2025 · 6 min read
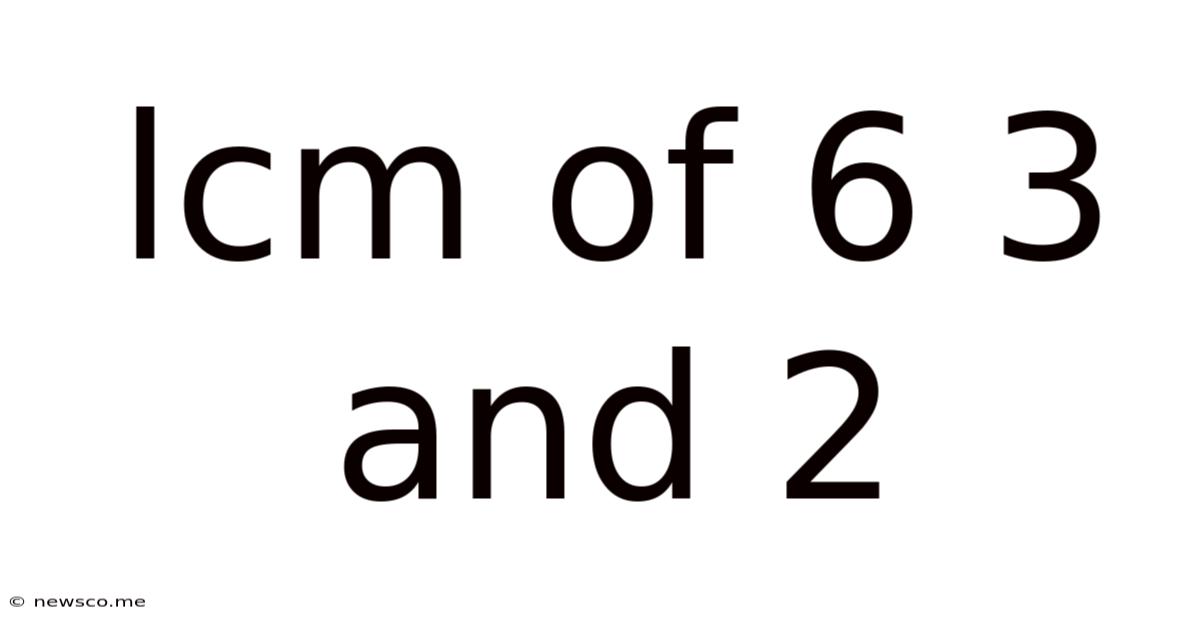
Table of Contents
Understanding the LCM of 6, 3, and 2: A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) is a fundamental concept in mathematics, particularly crucial in areas like fractions, algebra, and even programming. This article will explore the LCM of 6, 3, and 2 in detail, explaining various methods for calculating it and demonstrating its practical applications. We'll delve beyond the simple calculation and explore the underlying mathematical principles, making this a comprehensive guide for students and anyone wanting a deeper understanding of LCMs.
What is a Least Common Multiple (LCM)?
Before we tackle the specific numbers 6, 3, and 2, let's establish a solid understanding of the LCM itself. The least common multiple of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly. For example, the multiples of 2 are 2, 4, 6, 8, 10... and the multiples of 3 are 3, 6, 9, 12... The smallest number that appears in both lists is 6; therefore, the LCM of 2 and 3 is 6.
Calculating the LCM of 6, 3, and 2: Method 1 - Listing Multiples
The most straightforward method, especially for smaller numbers, is to list the multiples of each number until you find the smallest common multiple. Let's apply this to 6, 3, and 2:
- Multiples of 6: 6, 12, 18, 24, 30, 36...
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 36...
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36...
By inspecting the lists, we can see that the smallest number that appears in all three lists is 6. Therefore, the LCM of 6, 3, and 2 is 6.
Calculating the LCM of 6, 3, and 2: Method 2 - Prime Factorization
A more efficient method, particularly useful for larger numbers, involves prime factorization. This method involves breaking down each number into its prime factors. The LCM is then constructed by taking the highest power of each prime factor present in the factorizations.
Let's apply this to 6, 3, and 2:
- Prime factorization of 6: 2 x 3
- Prime factorization of 3: 3
- Prime factorization of 2: 2
The prime factors involved are 2 and 3. The highest power of 2 is 2¹ and the highest power of 3 is 3¹. Therefore, the LCM is 2¹ x 3¹ = 6.
Calculating the LCM of 6, 3, and 2: Method 3 - Greatest Common Divisor (GCD) Method
The LCM and the greatest common divisor (GCD) are closely related. There's a formula that connects them:
LCM(a, b) x GCD(a, b) = a x b
This formula can be extended to more than two numbers. While this method is more complex, it highlights the relationship between LCM and GCD.
First, let's find the GCD of 6, 3, and 2 using the Euclidean algorithm or prime factorization. The GCD of 6, 3, and 2 is 1 (as they share no common factors other than 1).
Let's denote the numbers as a=6, b=3, c=2. We can extend the formula to three numbers by finding the LCM of the LCM of two numbers and the third number.
First, find the LCM of 6 and 3. Using either method above, LCM(6,3) = 6.
Next, find the LCM of 6 and 2. LCM(6,2) = 6.
Therefore the LCM of 6, 3, and 2 is 6.
Understanding the Significance of the LCM
The LCM has several practical applications across various fields:
-
Fraction Addition and Subtraction: When adding or subtracting fractions with different denominators, finding the LCM of the denominators is crucial for finding a common denominator. This allows you to add or subtract the fractions easily.
-
Scheduling and Time Management: LCM is used to determine when events will occur simultaneously. For instance, if two buses arrive at a stop every 6 minutes and 3 minutes respectively, the LCM (6, 3) = 6 tells you they'll arrive together every 6 minutes.
-
Modular Arithmetic: In modular arithmetic (e.g., clock arithmetic), the LCM is frequently used in problems involving cycles and repetitions.
-
Music Theory: LCM plays a role in music theory when determining the least common multiple of note durations.
-
Computer Science: LCM is used in algorithms related to scheduling, synchronization, and resource allocation.
Exploring the Concept of Multiples Further
A multiple of a number is the product of that number and any integer. For example:
- Multiples of 6: 6, 12, 18, 24, 30, 36, ... (6 x 1, 6 x 2, 6 x 3, ...)
- Multiples of 3: 3, 6, 9, 12, 15, 18, ... (3 x 1, 3 x 2, 3 x 3, ...)
- Multiples of 2: 2, 4, 6, 8, 10, 12, ... (2 x 1, 2 x 2, 2 x 3, ...)
Understanding multiples is essential for grasping the concept of LCM. The LCM represents the smallest number that's simultaneously a multiple of all the given numbers.
Why is the LCM Important in Mathematics?
The LCM is a cornerstone of several mathematical concepts:
-
Foundation for Fraction Arithmetic: Without understanding LCM, performing operations with fractions becomes significantly more challenging. It forms the basis for finding common denominators, crucial for addition, subtraction, and comparison of fractions.
-
Modular Arithmetic and Congruences: LCM plays a key role in solving problems involving modular arithmetic, a branch of number theory with applications in cryptography and computer science.
-
Algebraic Simplification: LCM helps simplify algebraic expressions, particularly those involving fractions with variables.
-
Number Theory: The LCM is deeply intertwined with other concepts in number theory, such as GCD, prime factorization, and divisibility rules.
Advanced Applications and Extensions
The concept of LCM extends beyond the simple examples shown here. It finds applications in:
-
Abstract Algebra: LCM concepts have abstract counterparts in ring theory and ideal theory.
-
Cryptography: The LCM plays an indirect role in certain cryptographic algorithms where modular arithmetic is heavily used.
-
Signal Processing: In signal processing, LCM is useful in the analysis of periodic signals and their synchronization.
Conclusion: Mastering the LCM
Understanding the least common multiple is a foundational skill in mathematics with far-reaching applications. Whether you're a student tackling fractions or a professional working in a technical field, a solid grasp of the LCM, along with the various methods for calculating it, is invaluable. This article has provided a comprehensive overview, covering basic calculations, practical applications, and even touching upon its advanced uses. By mastering the LCM, you build a stronger mathematical foundation and open doors to a deeper understanding of numerous mathematical concepts.
Latest Posts
Related Post
Thank you for visiting our website which covers about Lcm Of 6 3 And 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.