Lcm Of 6 7 And 10
News Co
May 08, 2025 · 5 min read
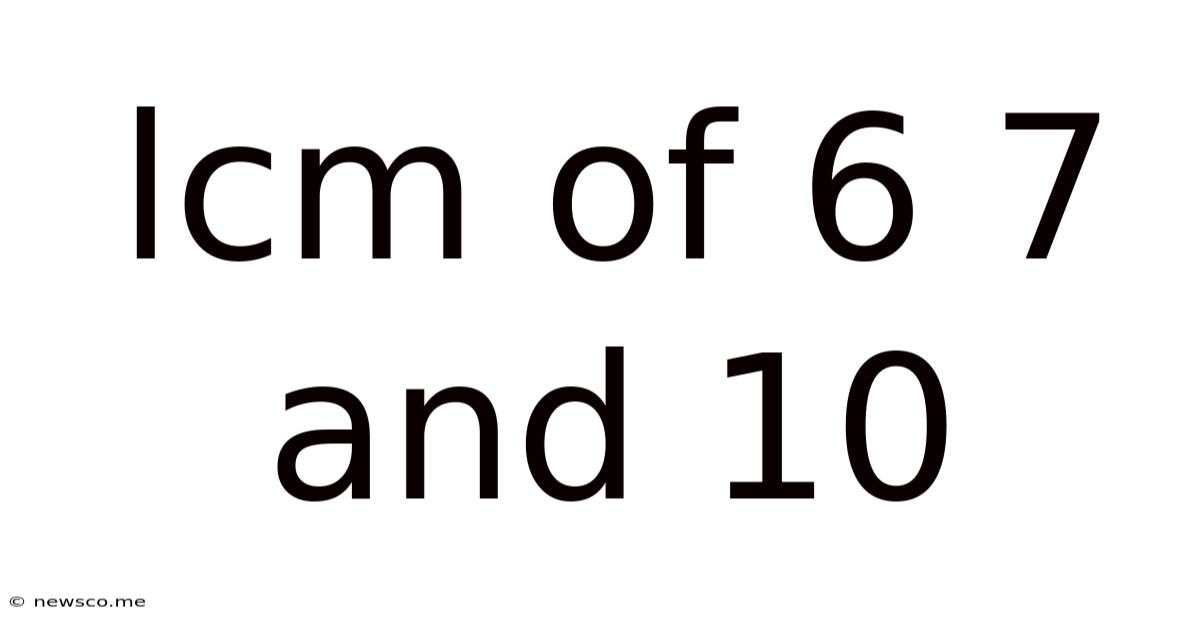
Table of Contents
Finding the LCM of 6, 7, and 10: A Comprehensive Guide
Finding the least common multiple (LCM) of a set of numbers is a fundamental concept in mathematics with applications across various fields, from scheduling to music theory. This article provides a comprehensive guide to calculating the LCM of 6, 7, and 10, exploring different methods and explaining the underlying principles. We'll also delve into the broader concept of LCM and its significance.
Understanding Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. In simpler terms, it's the smallest number that all the given numbers can divide into evenly. Understanding LCM is crucial for solving problems involving fractions, ratios, and cyclical events.
Why is LCM Important?
The applications of LCM are vast and varied. Here are a few key examples:
- Fraction addition and subtraction: Finding the LCM of the denominators is essential for adding or subtracting fractions with different denominators.
- Scheduling problems: Determining the time when two or more events will occur simultaneously often involves finding the LCM of the time intervals. For example, imagine two buses that arrive at a stop every 6 and 10 minutes respectively. The LCM helps determine when they will arrive together.
- Music theory: The LCM plays a role in determining musical intervals and harmonies.
- Cyclic processes: Many real-world processes, such as planetary orbits or machine cycles, are cyclical. The LCM helps find the time it takes for these cycles to align.
Methods for Calculating LCM
Several methods exist for calculating the LCM of a set of numbers. Let's explore the most common approaches, focusing on how to find the LCM of 6, 7, and 10.
1. Listing Multiples Method
This method involves listing the multiples of each number until a common multiple is found. While simple for small numbers, it becomes cumbersome for larger numbers.
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78, 84, 90, 96, 102, 108, 114, 120...
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98, 105, 112, 119, 126, 133, 140...
- Multiples of 10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120, 130, 140, 150...
By comparing the lists, we find that the smallest common multiple is 210. Therefore, the LCM(6, 7, 10) = 210.
2. Prime Factorization Method
This is a more efficient method, especially for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor.
- Prime factorization of 6: 2 × 3
- Prime factorization of 7: 7 (7 is a prime number)
- Prime factorization of 10: 2 × 5
To find the LCM, we take the highest power of each prime factor present in the factorizations:
- Highest power of 2: 2¹ = 2
- Highest power of 3: 3¹ = 3
- Highest power of 5: 5¹ = 5
- Highest power of 7: 7¹ = 7
Multiplying these together: 2 × 3 × 5 × 7 = 210. Therefore, the LCM(6, 7, 10) = 210.
3. Greatest Common Divisor (GCD) Method
The LCM and GCD (greatest common divisor) are related. The product of the LCM and GCD of two numbers is equal to the product of the two numbers. This relationship can be extended to more than two numbers, although the calculation becomes more complex.
First, let's find the GCD of 6, 7, and 10. Since 6, 7, and 10 share no common factors other than 1, their GCD is 1.
While this method isn't directly applicable to find the LCM of three numbers efficiently without using the prime factorization method, it highlights the relationship between LCM and GCD.
Step-by-Step Calculation of LCM(6, 7, 10) using Prime Factorization
Let's break down the prime factorization method step-by-step for clarity:
-
Find the prime factorization of each number:
- 6 = 2 × 3
- 7 = 7
- 10 = 2 × 5
-
Identify the unique prime factors: The unique prime factors are 2, 3, 5, and 7.
-
Determine the highest power of each unique prime factor:
- The highest power of 2 is 2¹ = 2
- The highest power of 3 is 3¹ = 3
- The highest power of 5 is 5¹ = 5
- The highest power of 7 is 7¹ = 7
-
Multiply the highest powers together: 2 × 3 × 5 × 7 = 210
Therefore, the LCM of 6, 7, and 10 is 210.
Practical Applications of LCM(6, 7, 10)
Let's consider some practical scenarios where understanding the LCM of 6, 7, and 10 is useful:
-
Scheduling: Imagine three events: Event A repeats every 6 days, Event B every 7 days, and Event C every 10 days. The LCM (210) represents the number of days until all three events occur on the same day again.
-
Fraction Operations: If you needed to add fractions with denominators of 6, 7, and 10, finding the LCM (210) would be crucial for finding a common denominator.
-
Cyclical Patterns: If three machines operate on cycles of 6, 7, and 10 units, respectively, the LCM helps to predict when all three machines will simultaneously complete a cycle.
Conclusion: Mastering LCM Calculations
Calculating the least common multiple is a valuable skill with diverse applications. The prime factorization method offers a robust and efficient approach, particularly when dealing with larger numbers. Understanding the concept of LCM is essential for problem-solving in various mathematical contexts and real-world situations. Remember, practice is key to mastering LCM calculations and applying them effectively. By understanding the methods outlined above, you can confidently tackle LCM problems and appreciate the significance of this fundamental mathematical concept. This comprehensive guide equips you with the knowledge and techniques to effectively determine the LCM of any set of numbers, fostering a deeper understanding of this important mathematical principle.
Latest Posts
Latest Posts
-
How To Find Height Of Trapezium
May 08, 2025
-
Matching Worksheets For 3 Year Olds Pdf
May 08, 2025
-
Use The Figure To Name Each Of The Following
May 08, 2025
-
How Many Glasses Is 1 5 Liters
May 08, 2025
-
Common Factors Of 35 And 50
May 08, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 6 7 And 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.