Lcm Of 6 8 And 4
News Co
Apr 08, 2025 · 5 min read
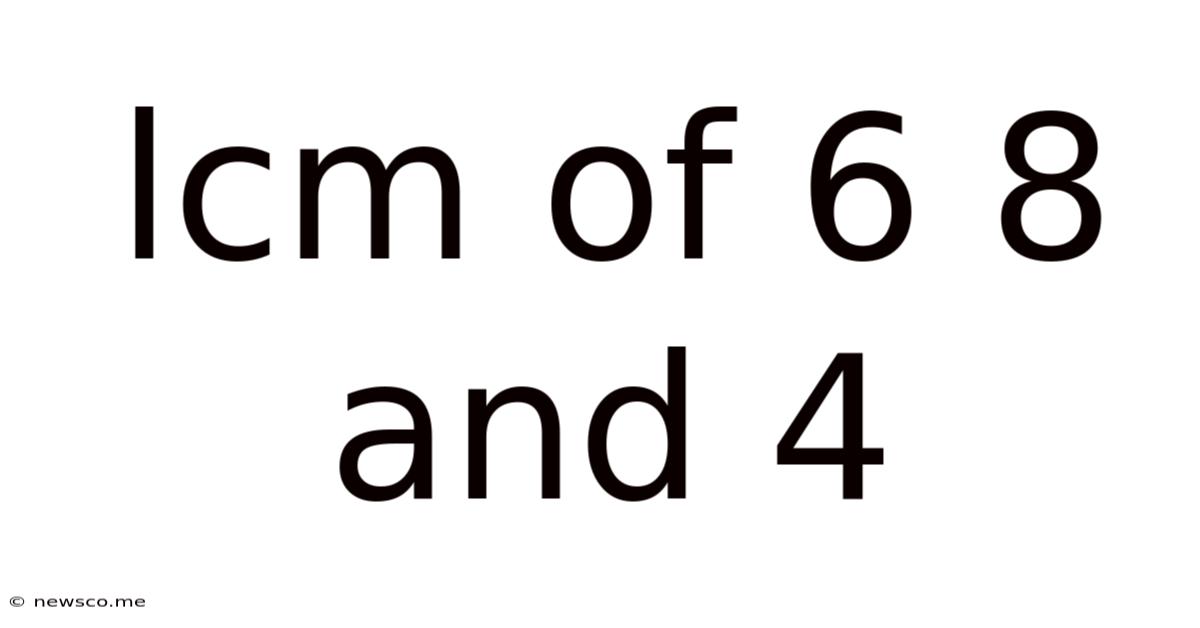
Table of Contents
Finding the LCM of 6, 8, and 4: A Comprehensive Guide
Finding the least common multiple (LCM) of a set of numbers is a fundamental concept in mathematics with applications spanning various fields, from scheduling and resource allocation to music theory and cryptography. This article delves deep into the process of calculating the LCM of 6, 8, and 4, exploring multiple methods and providing a comprehensive understanding of the underlying principles. We'll also examine the practical implications and broader applications of LCM calculations.
Understanding Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. It's a crucial concept for solving problems where we need to find a common point in time or a shared quantity. For instance, if you have three machines operating at different cycles (6, 8, and 4 units of time), the LCM tells you when they'll all be at the starting point simultaneously.
Key characteristics of LCM:
- Positive Integer: The LCM is always a positive integer.
- Divisibility: The LCM is divisible by each of the given integers.
- Minimality: It is the smallest positive integer satisfying the divisibility condition.
Methods for Calculating LCM(6, 8, 4)
There are several methods to calculate the LCM of 6, 8, and 4. Let's explore the most common ones:
1. Listing Multiples Method
This method involves listing the multiples of each number until we find the smallest common multiple.
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60...
- Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80...
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60...
By comparing the lists, we can see that the smallest common multiple is 24. Therefore, LCM(6, 8, 4) = 24.
This method is simple for smaller numbers but becomes cumbersome with larger numbers.
2. Prime Factorization Method
This is a more efficient method, especially for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor.
- Prime factorization of 6: 2 × 3
- Prime factorization of 8: 2³
- Prime factorization of 4: 2²
To find the LCM, we take the highest power of each prime factor present in the factorizations:
- Highest power of 2: 2³ = 8
- Highest power of 3: 3¹ = 3
Multiplying these together: 8 × 3 = 24. Therefore, LCM(6, 8, 4) = 24.
3. Greatest Common Divisor (GCD) Method
The LCM and GCD (greatest common divisor) of a set of numbers are related by the following formula:
LCM(a, b, c) = (|a × b × c|) / GCD(a, b, c)
This formula only works if we have a way to find the GCD of three numbers. One common approach to finding the GCD is through the Euclidean algorithm which is efficient for larger numbers.
- GCD(6, 8): Using the Euclidean algorithm or listing common divisors, we find GCD(6, 8) = 2.
- GCD(2, 4): Next, we find the GCD of the previous result and the remaining number: GCD(2, 4) = 2.
Therefore, GCD(6, 8, 4) = 2.
Now we apply the formula: LCM(6, 8, 4) = (6 × 8 × 4) / 2 = 192 / 2 = 24.
Comparing the Methods
Each method has its advantages and disadvantages:
- Listing Multiples: Simple for small numbers but inefficient for larger ones.
- Prime Factorization: Efficient for larger numbers but requires knowledge of prime factorization.
- GCD Method: Relatively efficient and leverages the relationship between LCM and GCD but requires calculating the GCD first.
Applications of LCM
The concept of LCM finds numerous applications across various disciplines:
1. Scheduling and Time Management
Imagine you have three tasks that take 6, 8, and 4 hours, respectively. The LCM(6, 8, 4) = 24 tells you that you can complete all three tasks together in the shortest time of 24 hours. This is essential for project planning and resource allocation.
2. Music Theory
LCM is used in music theory to determine the least common multiple of the rhythmic values in a musical piece, allowing musicians to synchronize their performance. For instance, the LCM helps determine when different instruments will play together in a harmonious rhythm.
3. Gear Ratios and Mechanical Engineering
In mechanical engineering, LCM helps determine gear ratios to ensure smooth and efficient power transmission. The LCM ensures the gears mesh correctly at the smallest possible interval.
4. Cyclic Processes and Patterns
LCM is crucial for analyzing cyclic processes or repeating patterns. For example, if three lights blink at intervals of 6, 8, and 4 seconds, their LCM will tell you when all three lights will blink simultaneously.
5. Number Theory and Cryptography
The concept of LCM plays a vital role in number theory, especially in the study of modular arithmetic. It forms the basis of several cryptographic algorithms used for secure data transmission.
Conclusion
Calculating the LCM of 6, 8, and 4 is a straightforward yet fundamental mathematical process with significant implications in various fields. While the listing multiples method is intuitive for small numbers, the prime factorization and GCD methods provide more efficient and scalable solutions for larger sets of numbers. Understanding the LCM helps solve practical problems related to scheduling, resource management, and the analysis of cyclical patterns, illustrating the profound reach of seemingly simple mathematical concepts. Mastering LCM calculation is an essential skill for students and professionals alike, enhancing problem-solving abilities in diverse contexts.
Latest Posts
Related Post
Thank you for visiting our website which covers about Lcm Of 6 8 And 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.