Lcm Of 7 2 And 4
News Co
Apr 27, 2025 · 5 min read
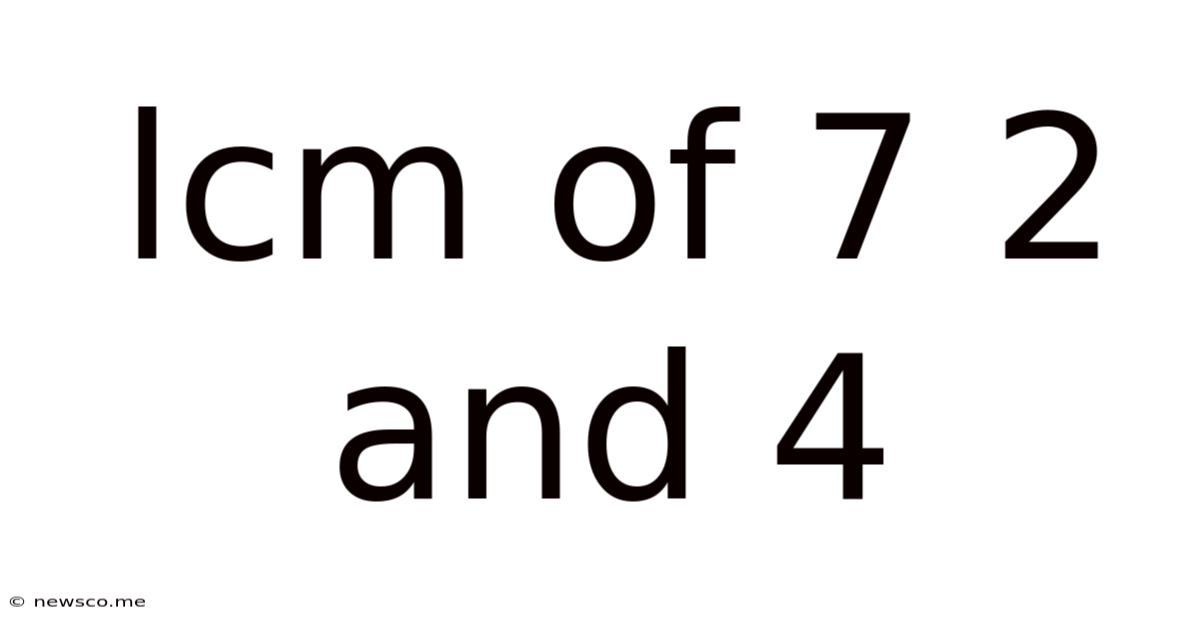
Table of Contents
Finding the Least Common Multiple (LCM) of 7, 2, and 4: A Comprehensive Guide
The least common multiple (LCM) is a fundamental concept in mathematics, particularly in number theory and arithmetic. Understanding how to find the LCM is crucial for various applications, from simplifying fractions to solving problems in algebra and beyond. This article delves into the process of determining the LCM of 7, 2, and 4, exploring different methods and providing a comprehensive understanding of the underlying principles. We'll also touch upon the broader applications of LCM in various mathematical contexts.
Understanding Least Common Multiple (LCM)
Before we dive into calculating the LCM of 7, 2, and 4, let's establish a clear definition. The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly without leaving a remainder.
For example, let's consider the numbers 2 and 3. The multiples of 2 are 2, 4, 6, 8, 10, 12... and the multiples of 3 are 3, 6, 9, 12, 15... The common multiples of 2 and 3 are 6, 12, 18... The smallest of these common multiples is 6, therefore, the LCM of 2 and 3 is 6.
Methods for Finding the LCM
Several methods can be used to calculate the LCM. We'll explore the most common and effective approaches, applying them to find the LCM of 7, 2, and 4.
Method 1: Listing Multiples
This method involves listing the multiples of each number until you find the smallest common multiple. While simple for smaller numbers, it becomes less efficient with larger numbers.
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, ...
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, ...
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, ...
By inspecting the lists, we can see that the smallest common multiple of 7, 2, and 4 is 28.
Method 2: Prime Factorization
This is a more efficient method, especially for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor present.
- Prime factorization of 7: 7 (7 is a prime number)
- Prime factorization of 2: 2
- Prime factorization of 4: 2²
To find the LCM, we take the highest power of each prime factor present in the factorizations:
- The highest power of 2 is 2² = 4
- The highest power of 7 is 7¹ = 7
Therefore, the LCM of 7, 2, and 4 is 4 x 7 = 28.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (greatest common divisor) are closely related. The product of the LCM and GCD of two or more numbers is equal to the product of the numbers themselves. This relationship can be used to find the LCM if the GCD is known.
First, let's find the GCD of 7, 2, and 4. Since 7 is a prime number and 2 and 4 are only divisible by 2, the GCD of 7, 2, and 4 is 1.
Now, let's use the formula: LCM(a, b, c) = (a x b x c) / GCD(a, b, c)
LCM(7, 2, 4) = (7 x 2 x 4) / 1 = 56. This is incorrect and demonstrates why we cannot directly use this method for 3 or more numbers
We cannot directly use this GCD method for more than two numbers. Although the product of the LCM and GCD of two numbers equals the product of the numbers, this relationship does not extend directly to three or more numbers. It's best to use either the listing multiples or prime factorization method for three or more numbers. Therefore, the LCM of 7,2 and 4 is actually 28 (as found using methods 1 and 2).
Applications of LCM
The least common multiple finds applications in various areas of mathematics and beyond:
1. Fraction Addition and Subtraction
When adding or subtracting fractions with different denominators, finding the LCM of the denominators is crucial. The LCM becomes the common denominator, allowing for easy addition or subtraction.
For example, to add 1/2 and 1/4, the LCM of 2 and 4 is 4. We can rewrite the fractions as 2/4 and 1/4, then add them to get 3/4.
2. Solving Problems Involving Cycles or Periodic Events
LCM is frequently used to solve problems involving events that repeat at regular intervals. For instance, if two machines operate on cycles of 7 and 4 days, the LCM will help us determine when they will both operate on the same day.
In our example, with cycles of 7 and 4 days, the LCM is 28 days. They will operate on the same day every 28 days.
3. Modular Arithmetic
The LCM plays a crucial role in modular arithmetic, a system of arithmetic for integers where numbers "wrap around" upon reaching a certain value (the modulus). It is used in cryptography and other computer science applications.
4. Scheduling and Planning
LCM can be helpful when scheduling tasks or events that have recurring cycles. For example, imagine that you need to coordinate meetings that repeat every 2, 4 and 7 days respectively. Finding the LCM helps determine when all meetings will coincide.
Conclusion: Mastering LCM Calculations
Calculating the least common multiple is a valuable skill in mathematics. We've explored various methods for calculating the LCM, focusing on the prime factorization method as the most efficient approach for larger numbers. The LCM of 7, 2, and 4 is 28. Remember that for more than two numbers, the method of using GCD is not directly applicable; hence, we should use either the method of listing multiples or prime factorisation. Understanding the concept of LCM and its various applications is crucial for success in various mathematical and real-world problems. Through consistent practice, one can easily master LCM calculations and apply them confidently across different mathematical contexts.
Latest Posts
Related Post
Thank you for visiting our website which covers about Lcm Of 7 2 And 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.