Lcm Of 7 4 And 3
News Co
Apr 21, 2025 · 4 min read
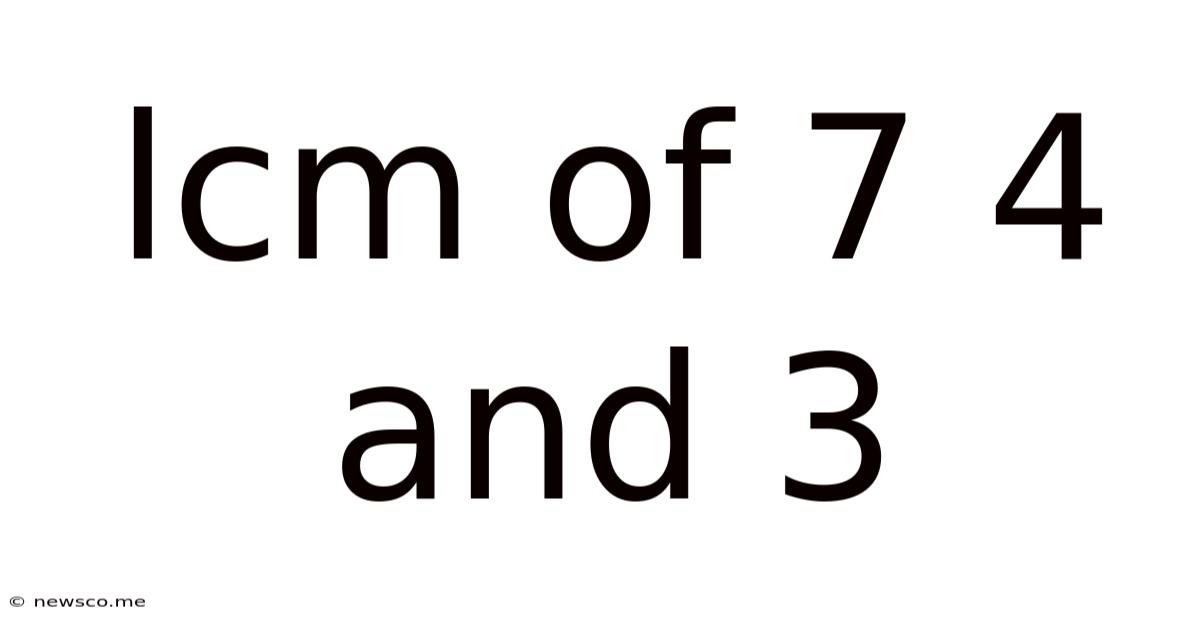
Table of Contents
Finding the Least Common Multiple (LCM) of 7, 4, and 3: A Comprehensive Guide
Finding the least common multiple (LCM) is a fundamental concept in mathematics with applications ranging from simple fraction addition to complex scheduling problems. This comprehensive guide will delve into the process of calculating the LCM of 7, 4, and 3, exploring different methods and providing a deeper understanding of the underlying principles. We'll also touch on the broader applications of LCMs and how understanding them can improve your mathematical problem-solving skills.
Understanding Least Common Multiples (LCM)
Before diving into the calculation, let's establish a clear understanding of what the LCM actually represents. The least common multiple of two or more numbers is the smallest positive integer that is divisible by all the numbers without leaving a remainder. In simpler terms, it's the smallest number that all the given numbers can divide evenly into.
For example, consider the numbers 2 and 3. The multiples of 2 are 2, 4, 6, 8, 10, 12... and the multiples of 3 are 3, 6, 9, 12, 15... The smallest number that appears in both lists is 6. Therefore, the LCM of 2 and 3 is 6.
Now, let's tackle the problem at hand: finding the LCM of 7, 4, and 3.
Method 1: Listing Multiples
This method is straightforward, especially for smaller numbers. We list the multiples of each number until we find the smallest multiple common to all three.
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, ...
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72, 76, 80, 84, ...
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 72, 75, 78, 81, 84, ...
By carefully examining the lists, we can see that the smallest number present in all three sequences is 84. Therefore, the LCM of 7, 4, and 3 is 84.
Method 2: Prime Factorization
This method is more efficient for larger numbers and provides a more systematic approach. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of all prime factors present.
-
Find the prime factorization of each number:
- 7 = 7 (7 is a prime number)
- 4 = 2²
- 3 = 3 (3 is a prime number)
-
Identify the unique prime factors: The unique prime factors are 2, 3, and 7.
-
Determine the highest power of each prime factor:
- The highest power of 2 is 2² = 4
- The highest power of 3 is 3¹ = 3
- The highest power of 7 is 7¹ = 7
-
Multiply the highest powers together: LCM(7, 4, 3) = 2² × 3 × 7 = 4 × 3 × 7 = 84
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (greatest common divisor) are closely related. There's a formula that connects them:
LCM(a, b) × GCD(a, b) = a × b
This formula can be extended to more than two numbers, although the calculation becomes more complex. While not the most direct method for finding the LCM of 7, 4, and 3, understanding this relationship is crucial for a comprehensive understanding of number theory.
Applications of LCM
The LCM has numerous applications across various fields:
-
Fraction Addition and Subtraction: Finding a common denominator when adding or subtracting fractions requires finding the LCM of the denominators.
-
Scheduling Problems: Determining when events will occur simultaneously, such as the meeting of buses at a station or the alignment of planets, often involves calculating the LCM of the periods or cycles.
-
Modular Arithmetic: LCM plays a critical role in solving problems related to congruences and modular arithmetic, which are used in cryptography and computer science.
-
Music Theory: LCM is used in understanding musical intervals and creating harmonious melodies. The frequencies of notes are often related through LCM calculations.
-
Engineering and Construction: The LCM is applied in various engineering applications such as determining the optimal time for the completion of tasks or the synchronization of machinery.
Why Understanding LCM is Important
Beyond the specific calculations, grasping the concept of LCM enhances your mathematical intuition and problem-solving skills. It helps you to:
-
Develop Number Sense: Understanding LCM strengthens your ability to work with numbers effectively, to recognize patterns, and to make estimations.
-
Improve Problem-Solving: Many real-world problems, from scheduling to resource allocation, can be effectively addressed using the LCM.
-
Strengthen Foundations: A firm understanding of LCM lays a solid foundation for more advanced mathematical concepts in algebra, number theory, and calculus.
Conclusion
Finding the LCM of 7, 4, and 3, as we've demonstrated, can be approached through multiple methods. While the method of listing multiples is suitable for smaller numbers, prime factorization offers a more efficient and generalizable approach for larger numbers. Understanding the relationship between LCM and GCD provides a deeper insight into number theory. The applications of LCM extend far beyond simple mathematical exercises, demonstrating its practical relevance in diverse fields. By mastering this fundamental concept, you enhance your mathematical abilities and equip yourself to tackle more complex problems with confidence. Remember, the key is to choose the method that best suits the numbers involved and to practice regularly to strengthen your understanding.
Latest Posts
Related Post
Thank you for visiting our website which covers about Lcm Of 7 4 And 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.