Lcm Of 8 12 And 15
News Co
Apr 13, 2025 · 5 min read
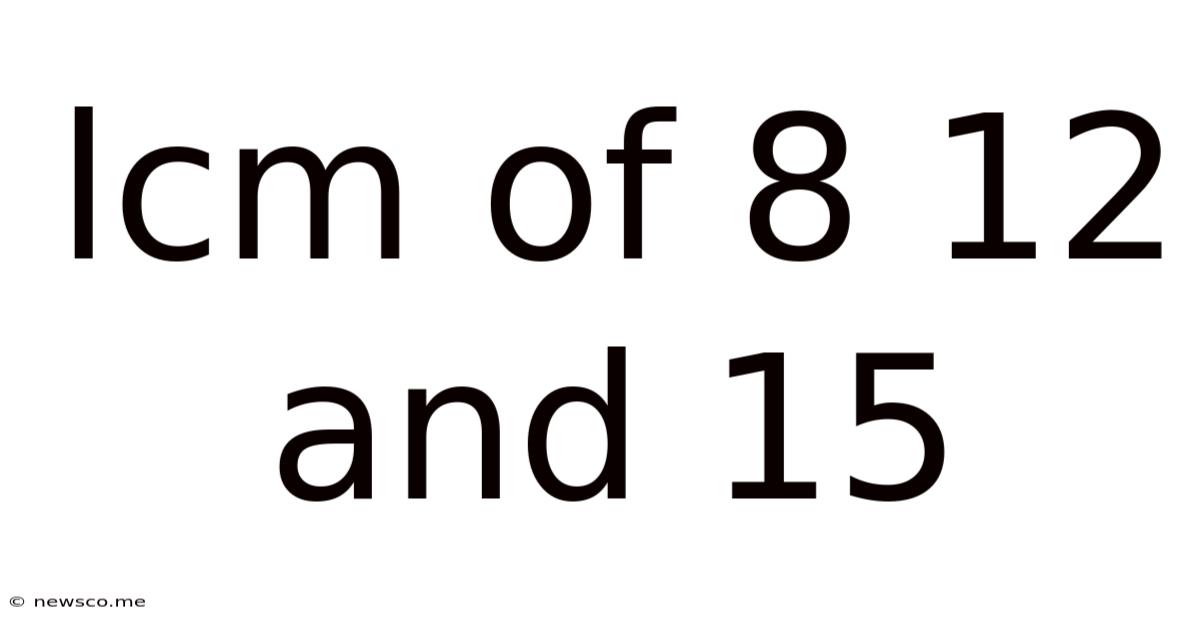
Table of Contents
Finding the LCM of 8, 12, and 15: A Comprehensive Guide
Finding the Least Common Multiple (LCM) of numbers is a fundamental concept in mathematics, crucial for various applications from simple fraction arithmetic to complex scheduling problems. This article will provide a comprehensive guide to calculating the LCM of 8, 12, and 15, exploring different methods and explaining the underlying principles. We will also delve into the practical applications of LCM calculations.
Understanding Least Common Multiples (LCM)
Before we tackle the specific problem of finding the LCM of 8, 12, and 15, let's solidify our understanding of what an LCM actually is. The LCM of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. Think of it as the smallest number that contains all the given numbers as factors.
For example, the LCM of 2 and 3 is 6 because 6 is the smallest positive integer that is divisible by both 2 and 3.
Method 1: Listing Multiples
This is a straightforward method, especially for smaller numbers. We list the multiples of each number until we find the smallest multiple common to all three.
- Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96, 104, 112, 120, ...
- Multiples of 12: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, ...
- Multiples of 15: 15, 30, 45, 60, 75, 90, 105, 120, ...
By inspecting the lists, we can see that the smallest common multiple of 8, 12, and 15 is 120.
Method 2: Prime Factorization
This method is more efficient, especially for larger numbers or when dealing with more than three numbers. It involves finding the prime factorization of each number and then constructing the LCM from these prime factors.
Let's find the prime factorization of each number:
- 8 = 2³ (8 is 2 x 2 x 2)
- 12 = 2² x 3 (12 is 2 x 2 x 3)
- 15 = 3 x 5 (15 is 3 x 5)
To find the LCM using prime factorization, we take the highest power of each prime factor present in the factorizations:
- The highest power of 2 is 2³ = 8
- The highest power of 3 is 3¹ = 3
- The highest power of 5 is 5¹ = 5
Now, multiply these highest powers together: 8 x 3 x 5 = 120
Therefore, the LCM of 8, 12, and 15 is 120.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (Greatest Common Divisor) are related through the following formula:
LCM(a, b) x GCD(a, b) = a x b
This formula can be extended to more than two numbers. However, it's often more complex to directly apply to three or more numbers. It’s generally more efficient to use prime factorization in such cases. While we can use this relationship, it might involve multiple steps of calculating GCD for pairs of numbers and then using the formula iteratively. For simplicity and efficiency with three numbers, the prime factorization method is preferred.
Practical Applications of LCM
The concept of LCM has numerous real-world applications across various fields:
1. Scheduling and Time Management:
Imagine you have three tasks that repeat at different intervals:
- Task A: Repeats every 8 days
- Task B: Repeats every 12 days
- Task C: Repeats every 15 days
To find out when all three tasks will coincide, you need to calculate the LCM of 8, 12, and 15. The LCM (120) indicates that all three tasks will coincide every 120 days.
2. Fraction Arithmetic:
Finding a common denominator when adding or subtracting fractions involves calculating the LCM of the denominators. For example, to add 1/8 + 1/12 + 1/15, you would find the LCM of 8, 12, and 15 (which is 120), and then rewrite each fraction with a denominator of 120 before adding them.
3. Gear Ratios and Mechanical Systems:
In mechanical engineering, LCM is used in designing gear systems and other machinery where components rotate at different speeds. The LCM helps determine the synchronization points and overall efficiency of the system.
4. Cyclic Processes:
Many natural and artificial processes are cyclical. Determining when cycles coincide requires LCM calculations. This is relevant in areas like astronomy (planetary alignments), biology (biological rhythms), and even manufacturing processes.
5. Number Theory:
LCM is a crucial concept in number theory, forming the foundation for many advanced mathematical theorems and concepts.
Beyond the Basics: Extending LCM Calculations
The methods discussed above can be extended to find the LCM of more than three numbers. The prime factorization method remains the most efficient approach for larger sets of numbers. For instance, to find the LCM of 8, 12, 15, and 20, you would find the prime factorization of each number and then take the highest power of each prime factor present.
- 8 = 2³
- 12 = 2² x 3
- 15 = 3 x 5
- 20 = 2² x 5
The highest powers are 2³, 3¹, and 5¹. Therefore, the LCM is 2³ x 3 x 5 = 120.
Conclusion: Mastering LCM Calculations
Calculating the least common multiple is a fundamental skill with broad applications across diverse fields. Understanding the different methods—listing multiples, prime factorization, and using the relationship with GCD—allows you to choose the most efficient approach depending on the numbers involved. The prime factorization method emerges as the most efficient and versatile technique, especially when dealing with larger numbers or multiple integers. By mastering these techniques, you equip yourself with a valuable tool for tackling various mathematical and real-world problems. Remember, practice is key to solidifying your understanding and improving your speed and accuracy in calculating LCMs.
Latest Posts
Related Post
Thank you for visiting our website which covers about Lcm Of 8 12 And 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.