Lcm Of 8 15 And 10
News Co
Mar 23, 2025 · 5 min read
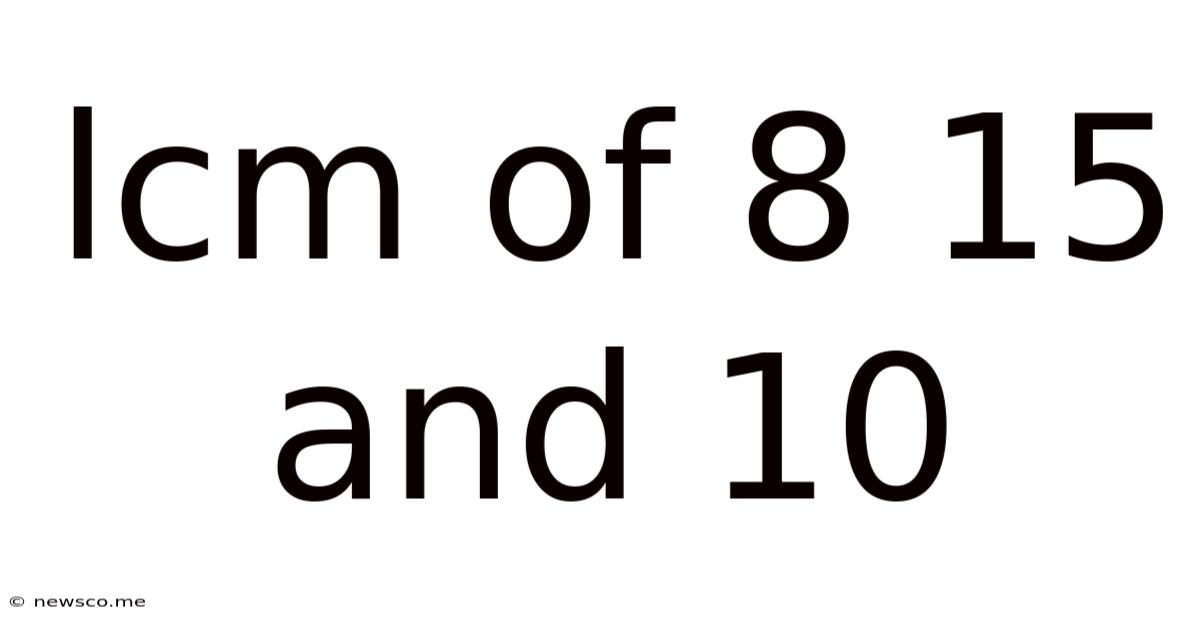
Table of Contents
Finding the LCM of 8, 15, and 10: A Comprehensive Guide
Finding the least common multiple (LCM) of numbers is a fundamental concept in mathematics with applications across various fields, from scheduling to music theory. This article delves into the process of calculating the LCM of 8, 15, and 10, exploring multiple methods and providing a comprehensive understanding of the underlying principles. We'll also discuss the significance of LCM and its real-world applications.
Understanding Least Common Multiple (LCM)
Before we tackle the specific numbers, let's define the LCM. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the given numbers as factors. For instance, the LCM of 2 and 3 is 6 because 6 is the smallest number divisible by both 2 and 3.
Method 1: Prime Factorization
This is arguably the most efficient method for finding the LCM of larger numbers, especially when dealing with more than two numbers. It involves breaking down each number into its prime factors.
Step 1: Prime Factorization of each number:
- 8: 2 x 2 x 2 = 2³
- 15: 3 x 5
- 10: 2 x 5
Step 2: Identify the highest power of each prime factor:
Looking at the prime factorizations above, we identify the distinct prime factors: 2, 3, and 5. Now, we find the highest power of each:
- Highest power of 2: 2³ = 8
- Highest power of 3: 3¹ = 3
- Highest power of 5: 5¹ = 5
Step 3: Multiply the highest powers:
To find the LCM, we multiply the highest powers of each prime factor together:
8 x 3 x 5 = 120
Therefore, the LCM of 8, 15, and 10 is 120.
Method 2: Listing Multiples
This method is straightforward but can become less efficient with larger numbers. It involves listing the multiples of each number until a common multiple is found.
Step 1: List multiples of each number:
- Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96, 104, 112, 120, 128...
- Multiples of 15: 15, 30, 45, 60, 75, 90, 105, 120, 135...
- Multiples of 10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120, 130...
Step 2: Identify the smallest common multiple:
By comparing the lists, we find that the smallest common multiple of 8, 15, and 10 is 120.
This method is effective for smaller numbers but becomes cumbersome and time-consuming as the numbers increase in size.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (Greatest Common Divisor) are related. We can use the GCD to find the LCM using the following formula:
LCM(a, b, c) = (a x b x c) / GCD(a, b, c)
However, this formula is most easily applied to two numbers. To extend this to three numbers, we need to apply it iteratively. First find the LCM of two of the numbers, then find the LCM of the result and the third number. This can be done in several ways.
Step 1: Find the GCD of 8 and 15
The GCD of 8 and 15 is 1, as they have no common factors other than 1.
Step 2: Find the LCM of 8 and 15
Using the formula: LCM(8, 15) = (8 x 15) / GCD(8, 15) = (8 x 15) / 1 = 120
Step 3: Find the GCD of 120 and 10
The GCD of 120 and 10 is 10.
Step 4: Find the LCM of 120 and 10
Using the formula: LCM(120, 10) = (120 x 10) / GCD(120, 10) = (120 x 10) / 10 = 120
Therefore, the LCM of 8, 15, and 10 is 120.
Real-World Applications of LCM
The concept of LCM has numerous practical applications in various fields:
-
Scheduling: Imagine you have three events – one occurring every 8 days, another every 15 days, and a third every 10 days. The LCM helps determine when all three events will coincide. In this case, they'll all occur simultaneously every 120 days.
-
Music: LCM plays a crucial role in music theory, particularly when dealing with rhythmic patterns and finding the least common denominator for different time signatures.
-
Construction and Engineering: In construction and engineering, LCM is used in determining the optimal timing for different tasks or processes that need to be synchronized.
-
Manufacturing: Production scheduling and inventory management often rely on LCM calculations to coordinate the production of different components or products with varying production cycles.
-
Computer Science: LCM is used in various algorithms and computations, including those related to synchronization and scheduling of tasks in parallel processing.
Conclusion: Mastering LCM Calculations
Finding the LCM, whether for a simple set of numbers like 8, 15, and 10 or a more complex set, is a valuable skill. Understanding the underlying principles and applying the appropriate method – prime factorization being the most robust – will significantly improve your mathematical proficiency. The examples and explanations provided in this article should equip you with the necessary knowledge to confidently tackle LCM problems in various contexts. Remember that the choice of method often depends on the numbers involved. For smaller numbers, listing multiples might be quicker, but for larger numbers, prime factorization is far more efficient and less prone to errors. The importance of LCM extends beyond theoretical mathematics, finding practical applications in numerous real-world scenarios, underscoring the significance of mastering this fundamental concept.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 8 15 And 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.