Lcm Of 8 6 And 10
News Co
Mar 24, 2025 · 5 min read
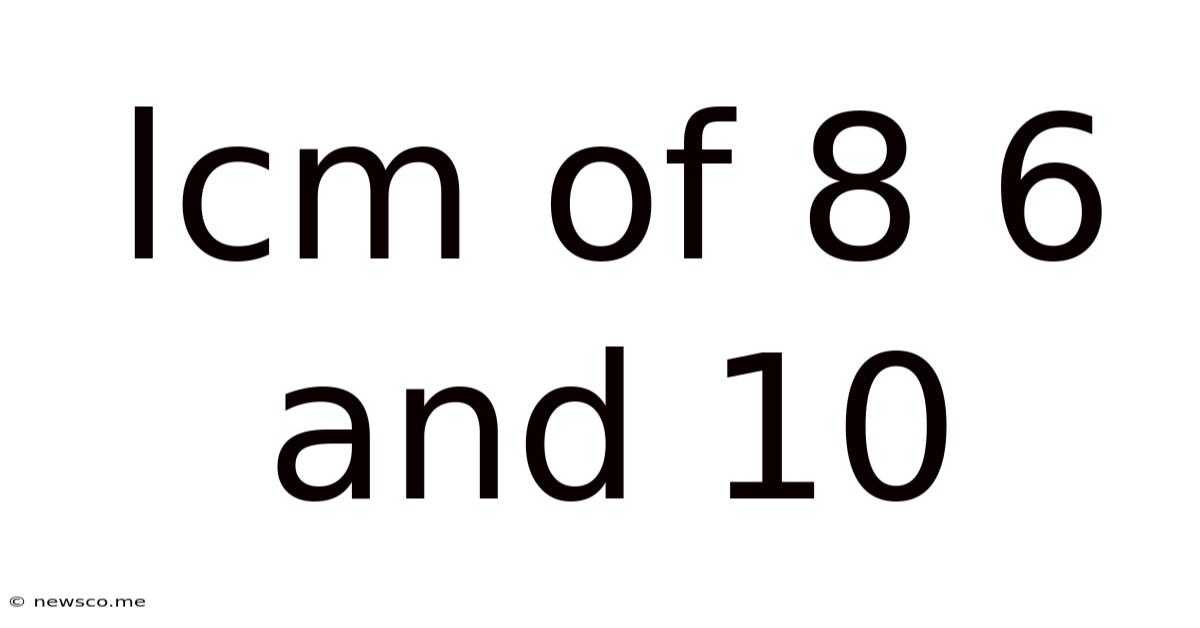
Table of Contents
Finding the Least Common Multiple (LCM) of 8, 6, and 10: A Comprehensive Guide
The least common multiple (LCM) is a fundamental concept in mathematics, particularly crucial in areas like fractions, number theory, and even practical applications like scheduling and resource management. This article will delve deep into finding the LCM of 8, 6, and 10, exploring various methods and illustrating the underlying principles. We'll go beyond a simple answer and equip you with the tools to calculate the LCM of any set of numbers efficiently.
Understanding Least Common Multiples
Before we tackle the specific problem of finding the LCM of 8, 6, and 10, let's solidify our understanding of what an LCM actually is. The LCM of two or more numbers is the smallest positive integer that is a multiple of all the numbers. In simpler terms, it's the smallest number that all the given numbers can divide into without leaving a remainder.
Example: Consider the numbers 2 and 3. Multiples of 2 are 2, 4, 6, 8, 10, 12... Multiples of 3 are 3, 6, 9, 12, 15... The smallest number that appears in both lists is 6, therefore, the LCM(2, 3) = 6.
Method 1: Listing Multiples
This method is straightforward, especially for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
Finding the LCM of 8, 6, and 10:
- Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96, 104, 112, 120...
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78, 84, 90, 96, 102, 108, 114, 120...
- Multiples of 10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120...
By inspecting the lists, we can see that the smallest number that appears in all three lists is 120. Therefore, the LCM(8, 6, 10) = 120.
Limitations of the Listing Method
While this method is intuitive, it becomes inefficient and impractical for larger numbers. Imagine trying to find the LCM of 144, 252, and 360 using this method. It would be extremely time-consuming and prone to errors. Hence, we need more efficient algorithms.
Method 2: Prime Factorization
This method is significantly more efficient, particularly for larger numbers. It relies on the fundamental theorem of arithmetic, which states that every integer greater than 1 can be represented uniquely as a product of prime numbers (excluding the order).
Steps:
-
Find the prime factorization of each number:
- 8 = 2 x 2 x 2 = 2³
- 6 = 2 x 3
- 10 = 2 x 5
-
Identify the highest power of each prime factor present:
- The prime factors are 2, 3, and 5.
- The highest power of 2 is 2³ = 8
- The highest power of 3 is 3¹ = 3
- The highest power of 5 is 5¹ = 5
-
Multiply the highest powers together:
- LCM(8, 6, 10) = 2³ x 3 x 5 = 8 x 3 x 5 = 120
Therefore, the LCM(8, 6, 10) = 120 using the prime factorization method.
Advantages of Prime Factorization
The prime factorization method is far more efficient and systematic than the listing method. It's easily adaptable to larger numbers and avoids the tedious process of generating extensive lists of multiples.
Method 3: Greatest Common Divisor (GCD) Method
The LCM and GCD (greatest common divisor) are closely related. There's a useful formula that connects them:
LCM(a, b) x GCD(a, b) = a x b
This formula works for two numbers. To extend it to three or more numbers, we can apply it iteratively. First, find the LCM of two numbers, then find the LCM of that result and the third number, and so on.
Finding the LCM of 8, 6, and 10 using the GCD method:
-
Find the GCD of 8 and 6 using the Euclidean algorithm:
- 8 = 6 x 1 + 2
- 6 = 2 x 3 + 0
- The GCD(8, 6) = 2
-
Find the LCM of 8 and 6:
- LCM(8, 6) = (8 x 6) / GCD(8, 6) = (48) / 2 = 24
-
Find the GCD of 24 and 10 using the Euclidean algorithm:
- 24 = 10 x 2 + 4
- 10 = 4 x 2 + 2
- 4 = 2 x 2 + 0
- The GCD(24,10) = 2
-
Find the LCM of 24 and 10:
- LCM(24, 10) = (24 x 10) / GCD(24, 10) = 240 / 2 = 120
Therefore, the LCM(8, 6, 10) = 120 using the GCD method.
This method demonstrates the interconnectedness of LCM and GCD, providing an alternative approach to calculating the LCM.
Applications of LCM
The concept of the least common multiple has numerous practical applications across various fields:
-
Scheduling: Determining when events will occur simultaneously. For example, if three buses arrive at a stop every 8, 6, and 10 minutes respectively, the LCM helps determine when they'll all arrive at the same time. In this case, they'll all be at the stop in 120 minutes.
-
Fractions: Finding the least common denominator (LCD) when adding or subtracting fractions. The LCD is simply the LCM of the denominators.
-
Gear Ratios: Calculating gear ratios in mechanical systems. LCM helps determine the synchronization of rotating parts.
-
Resource Allocation: Optimizing the use of resources, such as assigning tasks based on their time requirements, ensuring efficient use of manpower or equipment.
-
Cyclic Processes: Analyzing and synchronizing cyclical processes in various fields, such as electronics, engineering, and even biology.
Conclusion
Finding the LCM of 8, 6, and 10, while seemingly simple, provides a gateway to understanding broader mathematical concepts and their applications. We've explored three different methods: listing multiples, prime factorization, and the GCD method. Each method offers a unique approach, highlighting the versatility of mathematical tools. While the listing method is suitable for smaller numbers, prime factorization and the GCD method provide significantly more efficient and scalable solutions for larger and more complex problems. Understanding these methods allows you to tackle a wide range of problems involving LCM and appreciate the power and elegance of number theory. Remember to choose the method most suitable to the numbers involved for optimal efficiency. The understanding of LCM transcends simple calculations and finds real-world applicability across diverse disciplines.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 8 6 And 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.