Lcm Of 8 And 12 And 15
News Co
Apr 21, 2025 · 5 min read
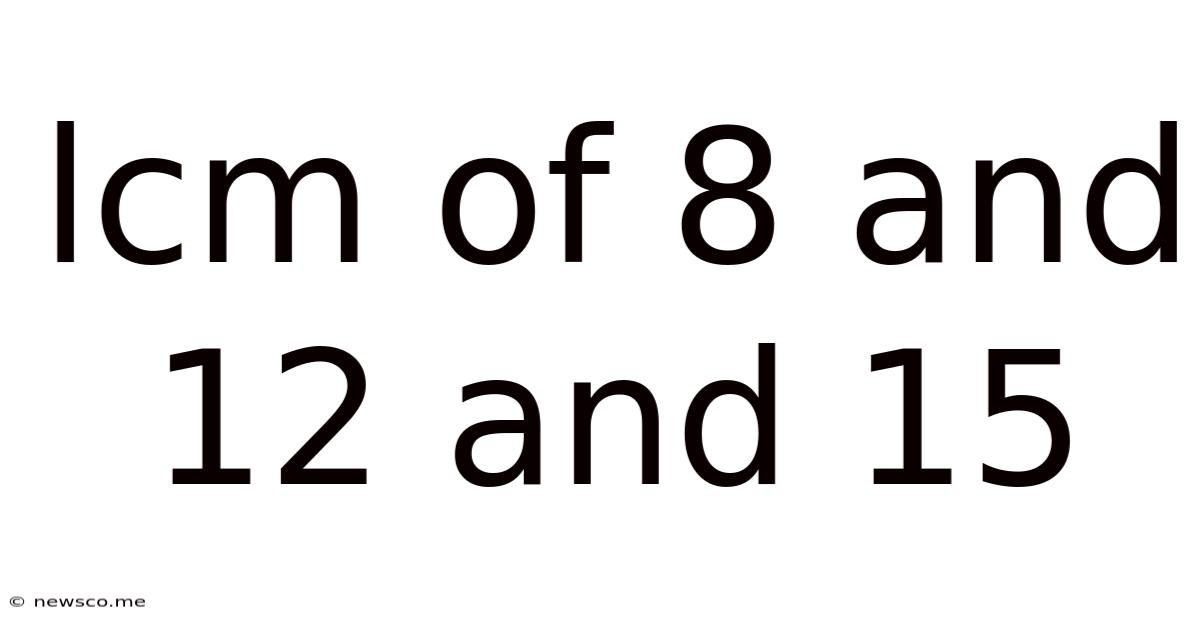
Table of Contents
- Lcm Of 8 And 12 And 15
- Table of Contents
- Finding the Least Common Multiple (LCM) of 8, 12, and 15: A Comprehensive Guide
- Understanding Least Common Multiples
- Method 1: Listing Multiples
- Finding Multiples of 8:
- Finding Multiples of 12:
- Finding Multiples of 15:
- Method 2: Prime Factorization
- Prime Factorization of 8:
- Prime Factorization of 12:
- Prime Factorization of 15:
- Method 3: Using the Greatest Common Divisor (GCD)
- Applications of LCM
- Scheduling and Project Management:
- Music Theory:
- Fraction Operations:
- Gear Ratios and Engineering:
- Cryptography:
- Conclusion: Mastering LCM Calculations
- Latest Posts
- Related Post
Finding the Least Common Multiple (LCM) of 8, 12, and 15: A Comprehensive Guide
The least common multiple (LCM) is a fundamental concept in mathematics with wide-ranging applications in various fields, from scheduling and project management to music theory and cryptography. Understanding how to calculate the LCM is crucial for solving problems involving fractions, ratios, and rhythmic patterns. This article provides a detailed explanation of how to find the LCM of 8, 12, and 15, exploring different methods and showcasing their practical applications.
Understanding Least Common Multiples
Before diving into the calculation, let's solidify our understanding of LCM. The LCM of two or more numbers is the smallest positive integer that is a multiple of all the numbers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly. This contrasts with the greatest common divisor (GCD), which is the largest number that divides all the given numbers without leaving a remainder.
For example, consider the numbers 4 and 6. The multiples of 4 are 4, 8, 12, 16, 20... and the multiples of 6 are 6, 12, 18, 24... The smallest number that appears in both lists is 12, therefore, the LCM of 4 and 6 is 12.
Method 1: Listing Multiples
This method is straightforward, especially for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
Finding Multiples of 8:
8, 16, 24, 32, 40, 48, 60, 72, 80, 96, 120, ...
Finding Multiples of 12:
12, 24, 36, 48, 60, 72, 84, 96, 108, 120, ...
Finding Multiples of 15:
15, 30, 45, 60, 75, 90, 105, 120, ...
By comparing the lists, we can see that the smallest number present in all three lists is 120. Therefore, the LCM of 8, 12, and 15 is 120. This method is effective for smaller numbers but becomes cumbersome for larger numbers.
Method 2: Prime Factorization
This method is more efficient and works well for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM from the prime factors.
Prime Factorization of 8:
8 = 2 x 2 x 2 = 2³
Prime Factorization of 12:
12 = 2 x 2 x 3 = 2² x 3
Prime Factorization of 15:
15 = 3 x 5
To find the LCM using prime factorization, we take the highest power of each prime factor present in the factorizations:
- The highest power of 2 is 2³ = 8
- The highest power of 3 is 3¹ = 3
- The highest power of 5 is 5¹ = 5
Now, we multiply these highest powers together:
LCM(8, 12, 15) = 2³ x 3 x 5 = 8 x 3 x 5 = 120
This method provides a more systematic and efficient approach, particularly when dealing with larger numbers.
Method 3: Using the Greatest Common Divisor (GCD)
There's a relationship between the LCM and GCD of two or more numbers. The product of the LCM and GCD of two numbers is equal to the product of the two numbers. This relationship can be extended to more than two numbers, but the calculation becomes more complex. While we can utilize this relationship, it's often more efficient to use prime factorization directly for multiple numbers.
Let's illustrate with two numbers first:
Let's find the LCM of 8 and 12 using the GCD.
First, we find the GCD of 8 and 12 using the Euclidean algorithm or prime factorization. The GCD(8,12) = 4.
Then, we use the formula: LCM(a, b) = (a x b) / GCD(a, b)
LCM(8, 12) = (8 x 12) / 4 = 24
Extending this to three numbers (8, 12, and 15) directly using the GCD is more involved and less efficient than prime factorization in this case.
Applications of LCM
The concept of LCM has numerous practical applications across various disciplines:
Scheduling and Project Management:
Imagine you have two machines that perform a task at different intervals. Machine A takes 8 hours, and Machine B takes 12 hours. To find when they will both complete the task simultaneously, you need to find the LCM(8, 12) = 24. They will both complete the task together after 24 hours.
Music Theory:
LCM is used to determine the least common denominator for musical rhythms and time signatures, helping composers and musicians synchronize different rhythmic patterns.
Fraction Operations:
Finding the LCM of the denominators is essential when adding or subtracting fractions with different denominators. This ensures that you have a common denominator before performing the operation.
Gear Ratios and Engineering:
In mechanical systems with gears, LCM helps calculate the rotational speeds and synchronization of different gears.
Cryptography:
LCM plays a role in some cryptographic algorithms and number theory applications.
Conclusion: Mastering LCM Calculations
Finding the LCM of numbers is a fundamental skill with far-reaching applications. This article explored three different methods for calculating the LCM, highlighting their strengths and weaknesses. The prime factorization method emerges as the most efficient and versatile technique, especially when dealing with multiple numbers or larger values. Understanding these methods empowers you to solve a wide range of problems involving multiples, fractions, rhythms, and various other aspects of mathematics and its applications in the real world. Remember to choose the method that best suits the complexity of the problem at hand. For smaller numbers, listing multiples might suffice, but for larger numbers and more complex scenarios, prime factorization provides a more efficient and reliable approach. Mastering LCM calculations is a cornerstone of mathematical proficiency and opens doors to deeper understanding across numerous fields.
Latest Posts
Related Post
Thank you for visiting our website which covers about Lcm Of 8 And 12 And 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.