Least Common Multiple Of 2 3 4
News Co
Mar 18, 2025 · 5 min read
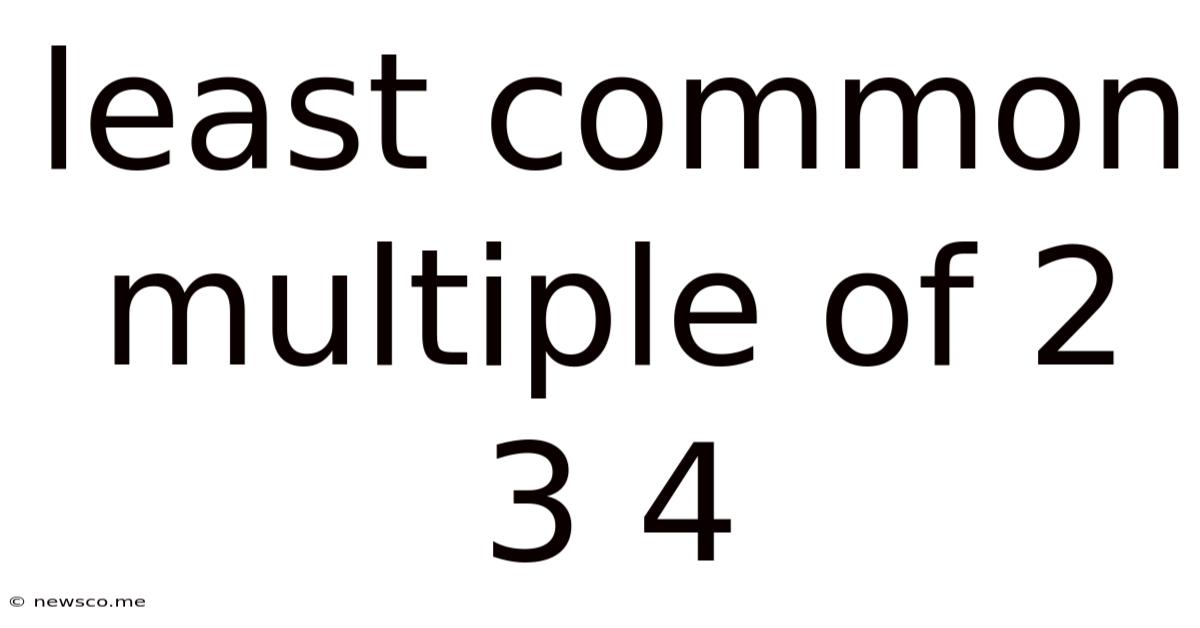
Table of Contents
Finding the Least Common Multiple (LCM) of 2, 3, and 4: A Comprehensive Guide
The least common multiple (LCM) is a fundamental concept in mathematics with wide-ranging applications. Understanding how to find the LCM is crucial for various mathematical operations, from simplifying fractions to solving complex equations. This article provides a comprehensive exploration of finding the LCM of 2, 3, and 4, explaining different methods and demonstrating their applications. We will delve into the theoretical underpinnings, practical calculations, and real-world examples to solidify your understanding.
What is the Least Common Multiple (LCM)?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. In simpler terms, it's the smallest number that all the given numbers can divide into evenly. For example, the LCM of 2 and 3 is 6 because 6 is the smallest number divisible by both 2 and 3.
Methods for Finding the LCM of 2, 3, and 4
Several methods can be used to determine the LCM, each with its own advantages and disadvantages. We'll examine three common approaches:
1. Listing Multiples Method
This method involves listing the multiples of each number until a common multiple is found.
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20...
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24...
- Multiples of 4: 4, 8, 12, 16, 20, 24...
By comparing the lists, we can see that the smallest common multiple is 12. Therefore, the LCM of 2, 3, and 4 is 12.
This method is straightforward for smaller numbers but becomes increasingly inefficient as the numbers get larger.
2. Prime Factorization Method
This method leverages the prime factorization of each number. Prime factorization is the process of expressing a number as a product of its prime factors (numbers divisible only by 1 and themselves).
- Prime factorization of 2: 2
- Prime factorization of 3: 3
- Prime factorization of 4: 2 x 2 = 2²
To find the LCM using prime factorization:
- Identify all the prime factors: In our case, the prime factors are 2 and 3.
- Find the highest power of each prime factor: The highest power of 2 is 2² (from the factorization of 4), and the highest power of 3 is 3¹ (from the factorization of 3).
- Multiply the highest powers together: 2² x 3¹ = 4 x 3 = 12
Therefore, the LCM of 2, 3, and 4 is 12 using the prime factorization method. This method is generally more efficient than the listing multiples method, especially for larger numbers.
3. Greatest Common Divisor (GCD) Method
The LCM and GCD (Greatest Common Divisor) are related through the following formula:
LCM(a, b) x GCD(a, b) = a x b
Where 'a' and 'b' are the numbers. This formula can be extended to more than two numbers. However, it's more complex to apply directly to three or more numbers and is often better suited for two numbers at a time. Let's illustrate this with our example:
-
Find the GCD of 2, 3, and 4: The GCD of 2, 3, and 4 is 1 (as there is no common divisor other than 1).
-
Use the LCM-GCD relationship (iteratively): While the direct formula doesn't cleanly extend to three numbers, we can apply it iteratively.
- Find LCM(2,3): Using the listing method or prime factorization, LCM(2,3) = 6.
- Now, find LCM(6,4): Using prime factorization, 6 = 2 x 3 and 4 = 2². The LCM(6,4) = 2² x 3 = 12.
Therefore, the LCM of 2, 3, and 4 is 12. This method, while effective, becomes more cumbersome as the number of integers increases.
Applications of LCM
The concept of LCM finds numerous applications in various fields:
1. Fraction Arithmetic
Finding a common denominator when adding or subtracting fractions requires finding the LCM of the denominators. For example, to add 1/2 + 1/3 + 1/4, we need the LCM of 2, 3, and 4, which is 12. This allows us to rewrite the fractions as 6/12 + 4/12 + 3/12 = 13/12.
2. Scheduling Problems
LCM is frequently used in scheduling problems. Imagine two machines operating on a cycle. One completes a cycle every 2 hours, the other every 3 hours, and a third every 4 hours. The LCM (12) represents the time when all three machines will complete a cycle simultaneously.
3. Number Theory
LCM plays a significant role in various number theory concepts, such as modular arithmetic and solving Diophantine equations.
4. Music Theory
In music, LCM helps determine the least common period of different musical rhythms.
5. Engineering and Construction
LCM is applied in designing and coordinating tasks in engineering and construction projects where different processes have different completion cycles.
Advanced Concepts and Extensions
While we've focused on finding the LCM of 2, 3, and 4, the principles extend to finding the LCM of larger sets of numbers and even non-integer values (though methods differ slightly).
- Finding LCM of larger sets of numbers: The prime factorization method remains the most efficient approach.
- Finding LCM of non-integer values: The concept extends to rational numbers; however, this often involves working with the least common denominator (LCD) and requires a slightly different approach.
- Computer algorithms for LCM: Efficient algorithms exist for computing the LCM of large numbers or sets of numbers, leveraging techniques like the Euclidean algorithm for GCD calculation.
Conclusion
Determining the LCM is a fundamental skill with significant practical applications across numerous disciplines. While the listing multiples method provides a straightforward approach for small numbers, the prime factorization method emerges as the most efficient and versatile technique, especially when dealing with larger numbers. Understanding the LCM's relationship with the GCD can also prove beneficial in specific scenarios. Mastering the LCM calculation equips you with a valuable tool for solving problems in mathematics, scheduling, and various other real-world contexts. The ability to calculate the LCM efficiently showcases a strong understanding of fundamental mathematical concepts and paves the way for tackling more advanced mathematical challenges. Remember to choose the method that best suits the given numbers and the complexity of the problem at hand. The understanding of this concept is crucial for anyone looking to develop a solid foundation in mathematics and its practical applications.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about Least Common Multiple Of 2 3 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.