Least Common Multiple Of 2 3 And 7
News Co
Apr 15, 2025 · 6 min read
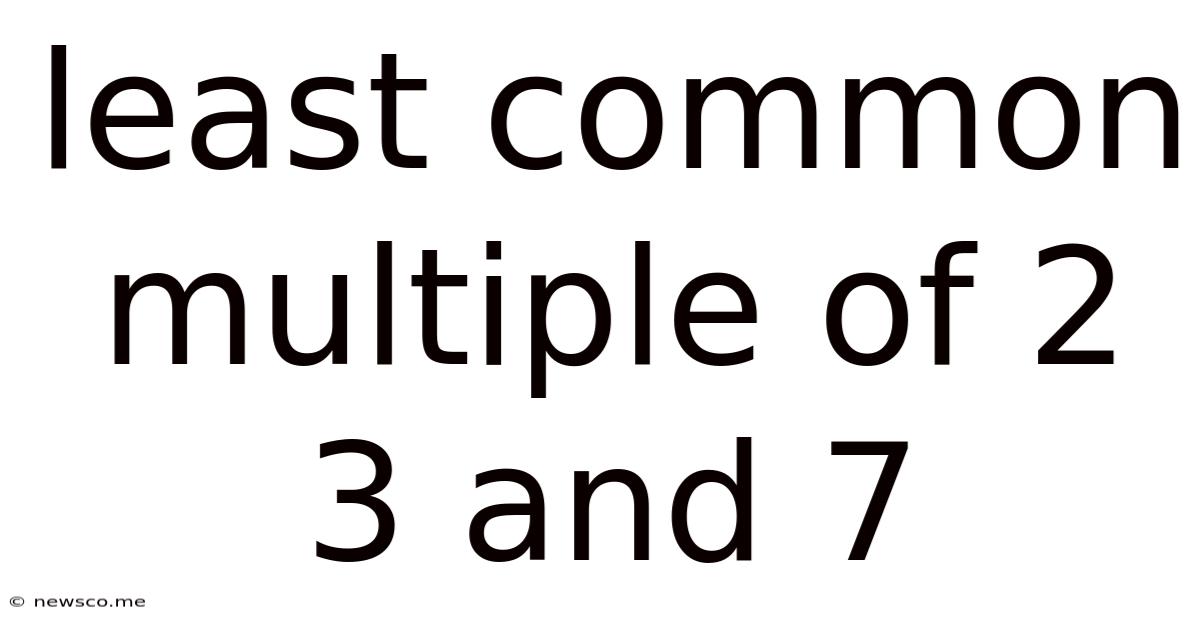
Table of Contents
Unveiling the Mysteries of the Least Common Multiple: A Deep Dive into 2, 3, and 7
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts and applying them to various scenarios can be surprisingly enriching. This comprehensive guide will delve into the LCM of 2, 3, and 7, exploring its calculation, applications, and broader implications within the realm of mathematics. We'll move beyond the basic formula and uncover the elegant connections between LCM, greatest common divisor (GCD), and prime factorization – essential tools in number theory and beyond.
Understanding the Fundamentals: Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. Think of it as the smallest number that's a common multiple for all the given numbers. For example, the LCM of 4 and 6 is 12, because 12 is the smallest number that's divisible by both 4 and 6.
This concept has far-reaching applications, from simplifying fractions and solving equations to scheduling tasks and understanding rhythmic patterns in music.
Why is LCM Important?
The significance of LCM extends beyond basic arithmetic:
- Fraction Simplification: Finding a common denominator when adding or subtracting fractions relies heavily on determining the LCM of the denominators.
- Scheduling Problems: Imagine two events occurring at regular intervals. The LCM helps determine when both events will coincide again. For instance, if one event happens every 2 days and another every 3 days, they'll coincide every 6 days (the LCM of 2 and 3).
- Modular Arithmetic: LCM plays a crucial role in understanding modular arithmetic, a branch of number theory used in cryptography and computer science.
- Music Theory: Rhythmic patterns in music often depend on LCM calculations to find the least common denominator of different note durations.
Calculating the LCM of 2, 3, and 7: Three Proven Methods
There are several methods to calculate the LCM, each offering a unique approach to the problem. Let's explore three popular techniques, applying them to our specific numbers: 2, 3, and 7.
Method 1: Prime Factorization
This method leverages the fundamental theorem of arithmetic, which states that every integer greater than 1 can be represented uniquely as a product of prime numbers.
-
Prime Factorize each number:
- 2 = 2
- 3 = 3
- 7 = 7
-
Identify the highest power of each prime factor: In this case, we have only the prime factors 2, 3, and 7, each appearing only once.
-
Multiply the highest powers together: 2 * 3 * 7 = 42
Therefore, the LCM of 2, 3, and 7 is 42.
This method is particularly efficient when dealing with larger numbers or sets of numbers, as it provides a systematic way to account for all prime factors.
Method 2: Listing Multiples
This method, while straightforward, can become cumbersome with larger numbers.
-
List multiples of each number:
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42, ...
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, ...
- Multiples of 7: 7, 14, 21, 28, 35, 42, ...
-
Identify the smallest common multiple: The smallest number appearing in all three lists is 42.
Therefore, the LCM of 2, 3, and 7 is 42.
This method is useful for visualizing the concept of LCM but is less efficient for larger numbers.
Method 3: Using the GCD (Greatest Common Divisor)
This method utilizes the relationship between LCM and GCD. The formula relating the two is:
LCM(a, b) * GCD(a, b) = a * b
This can be extended to more than two numbers, but the calculation becomes more complex. For three numbers, a, b, and c, there's no single elegant formula, but we can use it iteratively.
-
Find the GCD of any two numbers: Let's find the GCD of 2 and 3. Since 2 and 3 are prime and have no common factors other than 1, their GCD is 1.
-
Find the LCM of those two numbers: Using the formula above: LCM(2, 3) * GCD(2, 3) = 2 * 3. Since GCD(2,3) = 1, then LCM(2,3) = 6
-
Now find the LCM of the result and the third number: We need to find the LCM(6, 7). The GCD(6,7) is 1. Using the formula: LCM(6, 7) * GCD(6, 7) = 6 * 7. Therefore, LCM(6, 7) = 42
Therefore, the LCM of 2, 3, and 7 is 42.
This method highlights the interconnectedness of LCM and GCD, providing a deeper understanding of their relationship. While potentially more complex for multiple numbers, it reinforces the foundational principles of number theory.
Applications of the LCM of 2, 3, and 7
The LCM of 2, 3, and 7, which we've established to be 42, has practical applications in various scenarios:
-
Scheduling: Imagine three tasks needing to be performed: one every 2 days, one every 3 days, and one every 7 days. They will all coincide every 42 days.
-
Fraction Operations: If you needed to add or subtract fractions with denominators 2, 3, and 7, you would use 42 as the least common denominator.
-
Cyclic Patterns: This LCM could be relevant in analyzing cyclical processes where events repeat at intervals of 2, 3, and 7 units.
-
Modular Arithmetic Problems: In problems involving modular arithmetic with these moduli, understanding the LCM of 2, 3, and 7 simplifies computations.
Expanding the Concept: LCM and More Than Three Numbers
The methods described above can be extended to find the LCM of more than three numbers. The prime factorization method remains particularly efficient. You simply prime factorize each number, identify the highest power of each prime factor present, and then multiply these highest powers together.
For example, to find the LCM of 2, 3, 7, and 5:
- Prime factorize: 2 = 2, 3 = 3, 7 = 7, 5 = 5
- Highest powers: 2¹, 3¹, 5¹, 7¹
- Multiply: 2 * 3 * 5 * 7 = 210
The LCM of 2, 3, 7, and 5 is 210.
Conclusion: The Power of the Least Common Multiple
The seemingly simple concept of the least common multiple unlocks a world of mathematical possibilities. Understanding its calculation through different methods—prime factorization, listing multiples, and leveraging the relationship with GCD—provides a strong foundation for tackling more advanced mathematical problems. Its applications extend far beyond basic arithmetic, permeating areas like scheduling, fraction simplification, modular arithmetic, and even music theory. The exploration of the LCM of 2, 3, and 7 serves as a springboard to understanding this vital concept and its profound implications within mathematics and beyond. Mastering the LCM is not just about finding a number; it's about gaining a deeper appreciation for the structure and elegance of the number system itself.
Latest Posts
Related Post
Thank you for visiting our website which covers about Least Common Multiple Of 2 3 And 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.