Least Common Multiple Of 3 5 7
News Co
Apr 05, 2025 · 6 min read
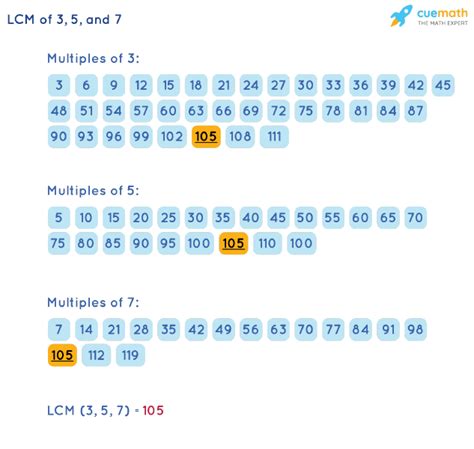
Table of Contents
Unveiling the Mysteries of the Least Common Multiple (LCM): A Deep Dive into 3, 5, and 7
Finding the least common multiple (LCM) might seem like a simple mathematical task, but understanding the underlying concepts and exploring different methods can unlock a deeper appreciation for number theory. This article delves into the LCM of 3, 5, and 7, exploring various approaches, highlighting their practical applications, and revealing the fascinating connections between seemingly simple numbers.
Understanding the Least Common Multiple (LCM)
Before we jump into the specifics of finding the LCM of 3, 5, and 7, let's establish a firm understanding of what the LCM actually represents. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. In simpler terms, it's the smallest number that all the given numbers can divide evenly into.
This concept is fundamental in various mathematical fields and has practical applications in diverse areas, from scheduling tasks to solving problems in engineering and computer science. Understanding LCM is crucial for efficiently solving problems involving fractions, ratios, and rhythmic patterns.
Method 1: Prime Factorization – A Fundamental Approach
The most fundamental method for calculating the LCM involves prime factorization. This method leverages the unique representation of any integer as a product of its prime factors. A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself.
Let's apply this method to find the LCM of 3, 5, and 7:
-
Find the prime factorization of each number:
- 3 = 3 (3 is already a prime number)
- 5 = 5 (5 is already a prime number)
- 7 = 7 (7 is already a prime number)
-
Identify the highest power of each prime factor: In this case, each number is a prime number itself, and the highest power of each is simply 1.
-
Multiply the highest powers together: The LCM is obtained by multiplying the highest powers of all the prime factors. In this case, it's 3 × 5 × 7 = 105.
Therefore, the least common multiple of 3, 5, and 7 is 105. This method provides a clear and methodical approach, easily applicable to larger sets of numbers, even those with multiple prime factors and repeated primes.
Method 2: Listing Multiples – A Visual Approach
Another straightforward method, especially useful for smaller numbers, is to list the multiples of each number until you find the smallest common multiple.
-
List the multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 72, 75, 78, 81, 84, 87, 90, 93, 96, 99, 102, 105...
-
List the multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100, 105...
-
List the multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98, 105...
By comparing the lists, we can see that the smallest number common to all three lists is 105. This method offers a visual understanding but becomes less efficient with larger numbers.
Method 3: Using the Formula – A Concise Approach
For two numbers, a and b, the LCM can be calculated using the formula: LCM(a, b) = (|a × b|) / GCD(a, b), where GCD is the greatest common divisor. This method can be extended for more than two numbers by finding the LCM of the first two, then finding the LCM of that result and the third number, and so on.
Since 3, 5, and 7 are all prime numbers, their greatest common divisor (GCD) is 1. Applying the formula repeatedly:
-
LCM(3, 5) = (3 × 5) / GCD(3, 5) = 15 / 1 = 15
-
LCM(15, 7) = (15 × 7) / GCD(15, 7) = 105 / 1 = 105
Therefore, the LCM of 3, 5, and 7 is 105. This method combines efficiency with the understanding of both LCM and GCD.
Practical Applications of LCM
The concept of LCM has far-reaching applications beyond the realm of pure mathematics. Here are a few examples:
1. Scheduling and Synchronization:
Imagine you have three different machines that complete a cycle every 3, 5, and 7 hours respectively. To determine when they will all be at the starting point of their cycles simultaneously, you need to find the LCM of 3, 5, and 7, which is 105 hours. This indicates that all machines will align at their starting point after 105 hours.
2. Fraction Operations:
When adding or subtracting fractions with different denominators, finding the LCM of the denominators is crucial. The LCM serves as the common denominator, simplifying the calculation. For example, adding 1/3, 1/5, and 1/7 requires finding the LCM of 3, 5, and 7 (105) to create a common denominator.
3. Rhythmic Patterns and Music:
In music and rhythmic patterns, LCM helps in determining when different rhythmic cycles coincide. For instance, if three instruments play patterns repeating every 3, 5, and 7 beats respectively, the LCM (105 beats) indicates when all patterns will simultaneously return to their starting points.
4. Gear Ratios and Engineering:
In mechanical engineering, gear ratios and the synchronization of rotating components often rely on understanding LCM. Determining the optimal gear ratios to achieve a desired speed or synchronization requires calculating the LCM of relevant gear teeth numbers.
5. Computer Science and Algorithms:
In computer science, LCM finds application in algorithms related to scheduling processes, managing resources, and optimizing data structures. Efficient computation of LCM is critical in these scenarios for optimal resource utilization and processing speed.
Expanding on LCM: Beyond Three Numbers
The methods described above can be generalized to find the LCM of any number of integers. The prime factorization method remains a powerful and robust approach, while the listing multiples method becomes less efficient with larger numbers or more integers. The iterative application of the formula involving GCD remains a viable alternative.
Conclusion: The Significance of the LCM of 3, 5, and 7
The seemingly simple task of finding the LCM of 3, 5, and 7 unveils a deeper understanding of fundamental mathematical principles. This seemingly small calculation has significant practical implications across numerous disciplines. From synchronizing machines to simplifying fractions and understanding rhythmic patterns, the LCM provides a powerful tool for solving real-world problems. This article has explored various methods for calculating the LCM, illustrating their strengths and limitations, and showcasing the wide-ranging applications of this important mathematical concept. Understanding LCM is not just about number crunching; it's about appreciating the interconnectedness of mathematical concepts and their relevance in diverse fields. The number 105, the LCM of 3, 5, and 7, represents more than just a mathematical result; it embodies a fundamental principle with far-reaching consequences.
Latest Posts
Related Post
Thank you for visiting our website which covers about Least Common Multiple Of 3 5 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.