Least Common Multiple Of 3 5 And 7
News Co
Apr 02, 2025 · 5 min read
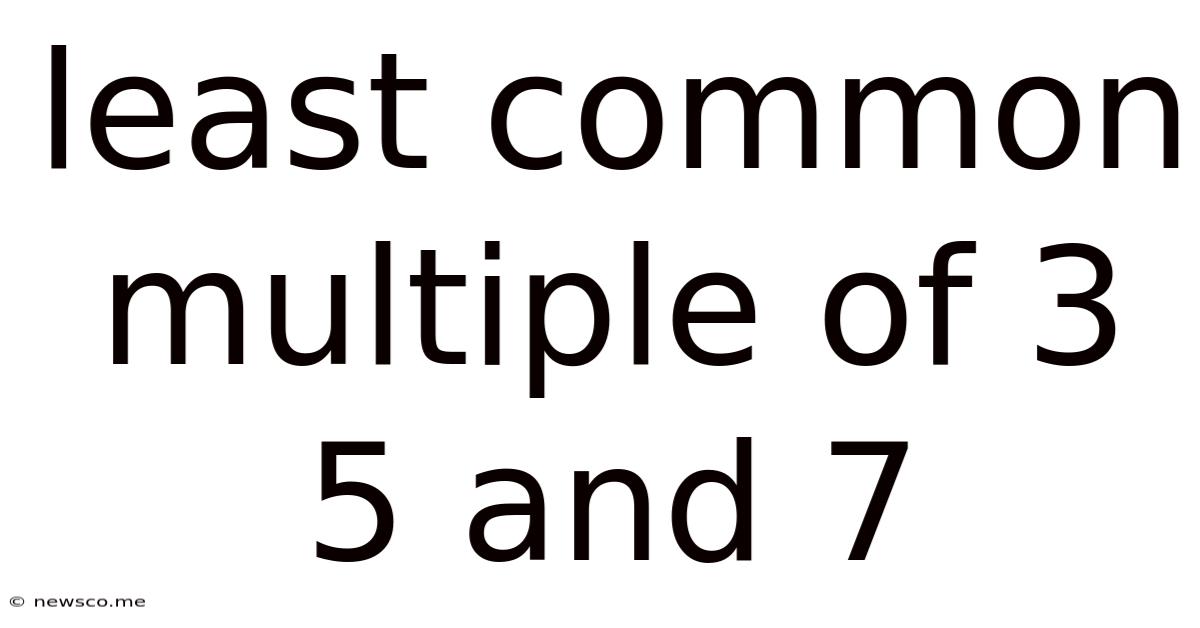
Table of Contents
Finding the Least Common Multiple (LCM) of 3, 5, and 7: A Deep Dive
The least common multiple (LCM) is a fundamental concept in number theory and arithmetic. It represents the smallest positive integer that is a multiple of all the given integers. Understanding how to find the LCM is crucial for various mathematical applications, from simplifying fractions to solving problems in algebra and beyond. This article will delve into the methods of calculating the LCM of 3, 5, and 7, explore its significance, and showcase its relevance in different contexts.
Understanding Least Common Multiples
Before diving into the specifics of finding the LCM of 3, 5, and 7, let's solidify our understanding of the core concept. The LCM of two or more integers is the smallest positive integer that is divisible by each of the given integers without leaving a remainder. For instance, the LCM of 2 and 3 is 6 because 6 is the smallest positive integer divisible by both 2 and 3.
Key characteristics of the LCM:
- Smallest Multiple: The LCM is always the smallest positive integer that satisfies the divisibility condition.
- Divisibility: It's crucial to remember that the LCM must be divisible by all the integers in the set.
- Positive Integer: The LCM is always a positive integer.
Methods for Calculating the LCM of 3, 5, and 7
Several methods exist to determine the LCM of a set of numbers. Let's explore the most common and efficient approaches, applying them to find the LCM of 3, 5, and 7.
Method 1: Listing Multiples
This method involves listing the multiples of each number until we find the smallest common multiple.
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 35, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 70, 72, 75, 78, 81, 84, 87, 90, 93, 96, 99, 102, 105...
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100, 105...
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98, 105...
By comparing these lists, we can see that the smallest common multiple is 105.
Method 2: Prime Factorization
This is a more efficient method, especially for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor.
-
Prime Factorization:
- 3 = 3¹
- 5 = 5¹
- 7 = 7¹
-
Constructing the LCM: Since 3, 5, and 7 are all prime numbers, the LCM is simply the product of these prime numbers.
LCM(3, 5, 7) = 3 × 5 × 7 = 105
Method 3: Using the Formula (for two numbers) and iterative approach for more than two.
While a direct formula for LCM of more than two numbers isn't readily available, we can extend the formula for two numbers iteratively. The formula for the LCM of two numbers a and b is:
LCM(a, b) = (|a × b|) / GCD(a, b)
Where GCD is the greatest common divisor. Since the GCD of 3, 5, and 7 is 1 (as they are all prime and have no common factors other than 1), we can apply this formula iteratively:
- Find LCM(3,5): (3 x 5) / GCD(3,5) = 15/1 = 15
- Find LCM(15,7): (15 x 7) / GCD(15,7) = 105/1 = 105
Significance and Applications of LCM
The LCM has far-reaching applications across various mathematical and real-world contexts.
Fraction Operations
Finding the LCM is essential when adding or subtracting fractions with different denominators. To add fractions, we need to find a common denominator, and the LCM provides the smallest such denominator, simplifying the calculations. For example:
1/3 + 1/5 + 1/7 = (35 + 21 + 15) / 105 = 71/105
Scheduling and Cyclical Events
LCM is invaluable in solving problems involving cyclical events that repeat at different intervals. Consider scenarios like:
- Machines operating: Three machines operate at intervals of 3, 5, and 7 hours, respectively. When will they all operate simultaneously again? The answer is the LCM(3, 5, 7) = 105 hours.
- Traffic lights: If three traffic lights cycle every 3, 5, and 7 minutes, finding the LCM helps determine when they will all be green simultaneously.
Music Theory
In music theory, LCM helps in determining the least common period for notes played on different instruments. If instruments play notes with frequencies that are multiples of 3, 5, and 7, their harmony is more consistent when LCM is considered.
Computer Science
In computer algorithms and programming, determining the LCM is often used in tasks related to synchronization and scheduling of processes.
Expanding on the Concept: LCM of More Numbers
The methods described above can be extended to find the LCM of more than three numbers. The prime factorization method remains particularly efficient. For instance, to find the LCM of 3, 5, 7, and 11:
-
Prime Factorization:
- 3 = 3¹
- 5 = 5¹
- 7 = 7¹
- 11 = 11¹
-
Constructing the LCM: LCM(3, 5, 7, 11) = 3 × 5 × 7 × 11 = 1155
The iterative approach using the formula for two numbers is also applicable. However, the efficiency might decrease as the number of integers increases.
Conclusion: The Ubiquity of LCM
The least common multiple is a seemingly simple concept but has profound implications across numerous fields. Understanding how to find the LCM of 3, 5, and 7, and more generally for any set of numbers, is a crucial skill for anyone working with mathematics, computer science, or any discipline involving cyclical or repetitive patterns. From simplifying fractions to synchronizing complex systems, the LCM provides a fundamental framework for solving problems and creating efficient solutions. The prime factorization method stands as a particularly powerful and efficient technique for calculating LCMs, particularly when dealing with larger sets of integers. Mastering this concept opens doors to a deeper appreciation of numerical relationships and their real-world applications.
Latest Posts
Related Post
Thank you for visiting our website which covers about Least Common Multiple Of 3 5 And 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.