Least Common Multiple Of 3 8
News Co
Mar 24, 2025 · 5 min read
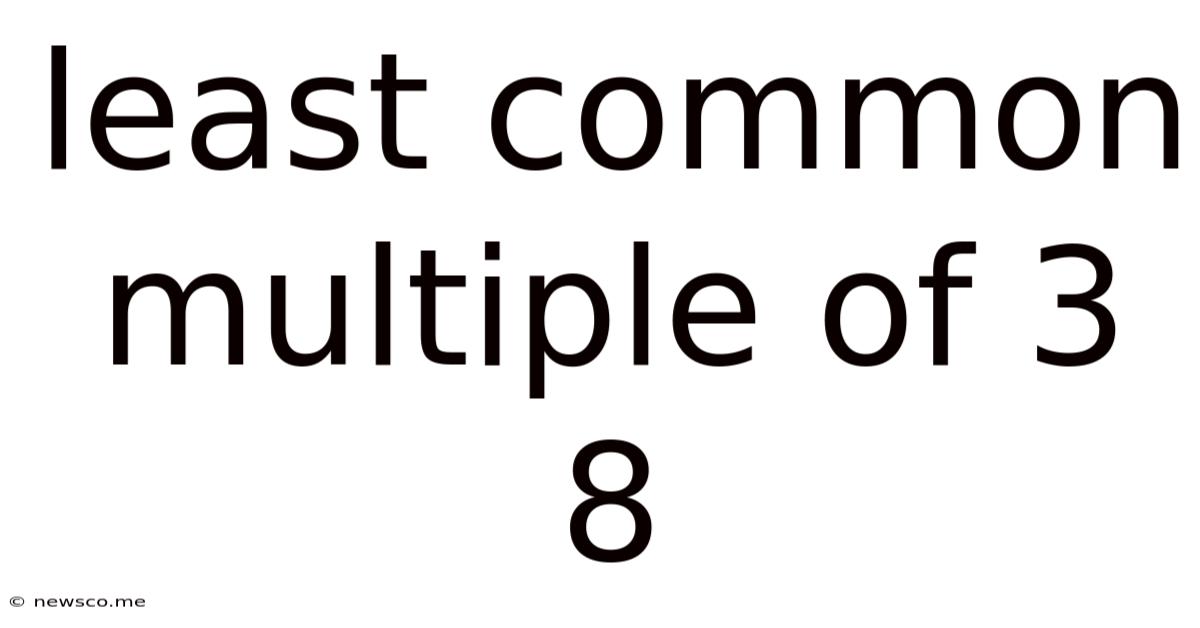
Table of Contents
Unveiling the Least Common Multiple (LCM) of 3 and 8: A Deep Dive
The concept of the Least Common Multiple (LCM) is a fundamental element in number theory and has far-reaching applications in various fields, from scheduling problems to musical harmony. This article delves deep into the calculation and significance of the LCM, focusing specifically on the LCM of 3 and 8. We’ll explore different methods for finding the LCM, discuss its properties, and uncover its practical relevance.
Understanding Least Common Multiples
Before we tackle the specific LCM of 3 and 8, let's establish a solid foundation. The Least Common Multiple (LCM) of two or more integers is the smallest positive integer that is a multiple of each of the numbers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly without leaving a remainder.
For example, consider the numbers 2 and 3. The multiples of 2 are 2, 4, 6, 8, 10, 12, and so on. The multiples of 3 are 3, 6, 9, 12, 15, and so on. The smallest number that appears in both lists is 6. Therefore, the LCM of 2 and 3 is 6.
Methods for Calculating the LCM
Several effective methods exist for determining the LCM of two or more numbers. Let's explore the most common techniques, illustrating each with examples relevant to our focus: the LCM of 3 and 8.
1. Listing Multiples Method
This straightforward method involves listing the multiples of each number until a common multiple is found. The smallest common multiple is the LCM.
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30...
- Multiples of 8: 8, 16, 24, 32, 40, 48...
Notice that 24 is the smallest number present in both lists. Therefore, the LCM(3, 8) = 24. This method is suitable for smaller numbers, but it becomes less efficient as the numbers increase in size.
2. Prime Factorization Method
This method leverages the prime factorization of each number. Prime factorization involves expressing a number as a product of its prime factors.
- Prime factorization of 3: 3 (3 is a prime number)
- Prime factorization of 8: 2 x 2 x 2 = 2³
To find the LCM using prime factorization, we identify the highest power of each prime factor present in the factorizations.
- The highest power of 2 is 2³ = 8
- The highest power of 3 is 3¹ = 3
Multiply these highest powers together: 8 x 3 = 24. Therefore, the LCM(3, 8) = 24. This method is generally more efficient than the listing method, especially for larger numbers.
3. Greatest Common Divisor (GCD) Method
The LCM and the Greatest Common Divisor (GCD) of two numbers are closely related. The product of the LCM and GCD of two numbers is equal to the product of the two numbers. This relationship is expressed as:
LCM(a, b) x GCD(a, b) = a x b
To use this method, we first need to find the GCD of 3 and 8. Since 3 and 8 have no common factors other than 1, their GCD is 1.
Now, we can apply the formula:
LCM(3, 8) x GCD(3, 8) = 3 x 8 LCM(3, 8) x 1 = 24 LCM(3, 8) = 24
This method is particularly useful when dealing with larger numbers where finding the GCD is computationally easier than directly finding the LCM. The Euclidean algorithm is a very efficient method for calculating the GCD.
Properties of the LCM
The LCM possesses several important properties:
- Commutative Property: LCM(a, b) = LCM(b, a) The order of the numbers doesn't affect the result.
- Associative Property: LCM(a, LCM(b, c)) = LCM(LCM(a, b), c) The grouping of numbers doesn't affect the result.
- Identity Property: LCM(a, 1) = a The LCM of any number and 1 is the number itself.
- Distributive Property: LCM(a, b) x GCD(a, b) = a x b (as demonstrated above)
These properties are crucial for simplifying calculations and solving problems involving LCMs.
Applications of the LCM
The concept of the LCM finds applications in various fields:
1. Scheduling Problems
Imagine two buses depart from a station at regular intervals. One bus departs every 3 hours, and the other departs every 8 hours. The LCM(3, 8) = 24 determines when both buses will depart simultaneously again. They will both depart at the same time after 24 hours.
2. Fraction Arithmetic
When adding or subtracting fractions with different denominators, finding the LCM of the denominators is essential to find a common denominator. This simplifies the calculation.
3. Music Theory
The LCM plays a role in music theory, determining the least common multiple of the lengths of musical phrases or patterns to determine when they repeat simultaneously.
4. Gear Ratios
In mechanical engineering, the LCM helps determine the rotational speeds of gears with different numbers of teeth.
5. Cyclic Events
The LCM is useful for predicting the next occurrence of cyclic events that happen at different intervals. For example, predicting when certain planets will align.
Advanced Concepts and Extensions
The concept of LCM extends beyond two numbers. We can calculate the LCM of three or more numbers using the same methods, particularly the prime factorization method. For instance, to find the LCM(3, 8, 5), we'd find the prime factorization of each number (3, 2³, 5) and then multiply the highest powers of each prime factor: 2³ x 3 x 5 = 120. The LCM(3, 8, 5) = 120.
Conclusion: The Significance of LCM(3, 8) = 24
The LCM of 3 and 8, calculated to be 24 using various methods, provides a practical example of this fundamental concept. Understanding the LCM is crucial for solving a wide array of problems across diverse disciplines. From simple scheduling scenarios to complex engineering applications, the concept provides a powerful tool for understanding and predicting cyclical patterns and synchronizing events. By mastering the different methods for calculating the LCM and understanding its properties, you equip yourself with a valuable skill set applicable in numerous contexts. This comprehensive exploration of the LCM of 3 and 8 serves as a springboard to deeper investigations into number theory and its practical implications.
Latest Posts
Related Post
Thank you for visiting our website which covers about Least Common Multiple Of 3 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.