Least Common Multiple Of 3 9 15
News Co
Apr 20, 2025 · 5 min read
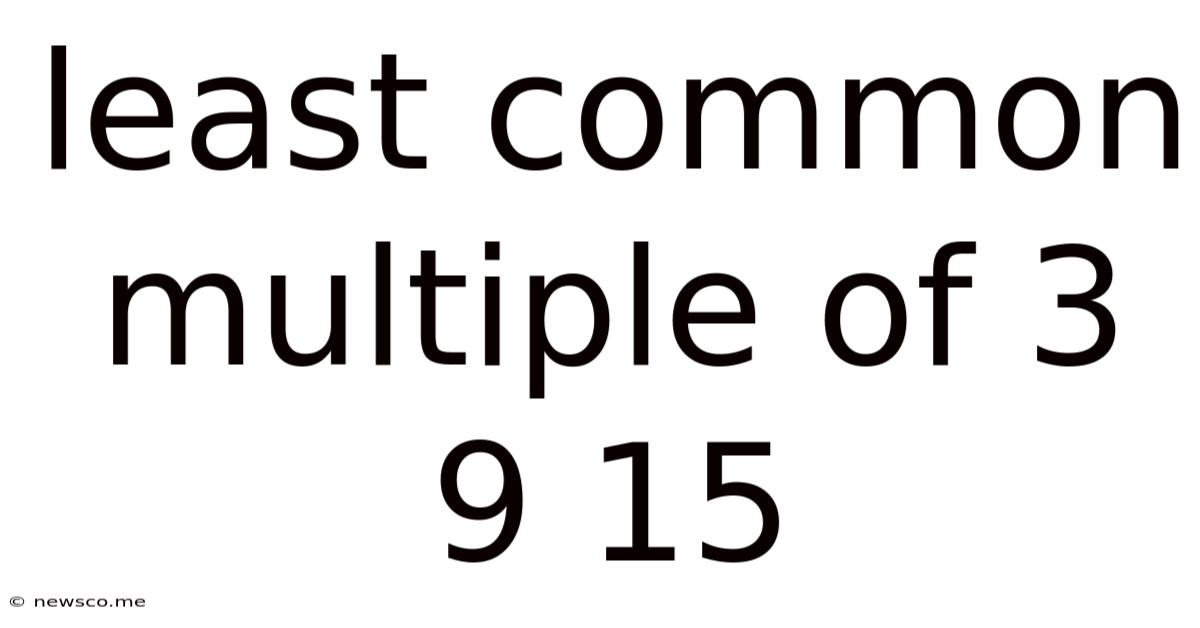
Table of Contents
Finding the Least Common Multiple (LCM) of 3, 9, and 15: A Comprehensive Guide
The least common multiple (LCM) is a fundamental concept in mathematics, particularly in number theory and arithmetic. Understanding LCM is crucial for various applications, from simplifying fractions to solving problems involving cyclical events. This article will delve into the methods of finding the LCM, specifically focusing on the numbers 3, 9, and 15, and then explore broader applications and related concepts.
Understanding Least Common Multiple (LCM)
The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly. For example, the LCM of 2 and 3 is 6, because 6 is the smallest number divisible by both 2 and 3.
Why is LCM important?
LCM has numerous applications across various fields:
- Fraction Addition and Subtraction: Finding a common denominator when adding or subtracting fractions requires finding the LCM of the denominators.
- Scheduling Problems: Determining when events with different periodicities will occur simultaneously (e.g., buses arriving at a stop).
- Gear Ratios and Mechanical Engineering: Calculating gear ratios and understanding the synchronization of rotating components.
- Modular Arithmetic: Solving congruence problems and analyzing cyclical patterns.
Methods for Finding the LCM of 3, 9, and 15
There are several ways to calculate the LCM, each with its own advantages and disadvantages. Let's explore the most common methods, applying them to find the LCM of 3, 9, and 15.
Method 1: Listing Multiples
This is the most straightforward method, especially for smaller numbers. We list the multiples of each number until we find the smallest multiple common to all.
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, ...
- Multiples of 9: 9, 18, 27, 36, 45, ...
- Multiples of 15: 15, 30, 45, 60, ...
Observing the lists, we see that the smallest multiple common to 3, 9, and 15 is 45. Therefore, the LCM(3, 9, 15) = 45.
Method 2: Prime Factorization
This method is more efficient for larger numbers. We find the prime factorization of each number and then construct the LCM using the highest powers of all prime factors present.
- Prime factorization of 3: 3¹
- Prime factorization of 9: 3²
- Prime factorization of 15: 3¹ * 5¹
To find the LCM, we take the highest power of each prime factor present in the factorizations:
- Highest power of 3: 3² = 9
- Highest power of 5: 5¹ = 5
Therefore, LCM(3, 9, 15) = 3² * 5¹ = 9 * 5 = 45
Method 3: Greatest Common Divisor (GCD) Method
This method utilizes the relationship between LCM and GCD (greatest common divisor). The formula is:
LCM(a, b, c) = (|a * b * c|) / GCD(a, b, c)
First, we need to find the GCD of 3, 9, and 15. The GCD is the largest number that divides all three numbers evenly. In this case, the GCD(3, 9, 15) = 3.
Now, applying the formula:
LCM(3, 9, 15) = (3 * 9 * 15) / 3 = 405 / 3 = 45
This method is particularly useful when dealing with larger numbers, as finding the GCD is often easier than directly finding the LCM.
Extending the Concept: LCM of More Than Three Numbers
The methods described above can be extended to find the LCM of more than three numbers. For the prime factorization method, you simply include all prime factors and their highest powers from the factorization of each number. For the listing multiples method, the process becomes more tedious but remains conceptually the same. The GCD method also extends readily to multiple numbers using a suitable GCD algorithm.
Applications of LCM: Real-World Examples
Let's explore some real-world scenarios where understanding LCM is essential:
Scenario 1: Synchronizing Traffic Lights
Imagine three traffic lights at intersections A, B, and C. Light A cycles every 30 seconds, light B every 45 seconds, and light C every 60 seconds. To determine when all three lights will simultaneously be green, we need to find the LCM of 30, 45, and 60. This will tell us the time interval after which all lights will be green at the same time.
Scenario 2: Scheduling Tasks
Suppose you have three tasks to complete: Task A takes 15 minutes, Task B takes 20 minutes, and Task C takes 25 minutes. You want to determine the shortest time interval in which all three tasks can be completed an integer number of times. This requires finding the LCM of 15, 20, and 25.
Scenario 3: Manufacturing and Production
In manufacturing, LCM is vital in optimizing production schedules and coordinating the operation of different machines. For instance, consider machines producing parts at different rates. The LCM helps determine when a synchronized production cycle can be achieved.
Advanced Concepts and Related Topics
While we've focused on the basic methods of finding the LCM, it's beneficial to briefly touch upon more advanced related topics:
- Euclidean Algorithm: A highly efficient algorithm for computing the GCD of two integers, which is crucial for the GCD method of finding the LCM.
- Least Common Multiple of Polynomials: The concept of LCM extends beyond integers to polynomials, playing a key role in algebraic manipulations and fraction simplification.
- Modular Arithmetic and LCM: LCM finds significant application in solving problems in modular arithmetic, relating to congruences and cyclical patterns.
Conclusion
Finding the least common multiple is a fundamental skill with wide-ranging applications across mathematics and various real-world scenarios. Mastering the different methods, from listing multiples to using prime factorization or the GCD method, empowers you to tackle a variety of problems efficiently and effectively. Understanding the underlying principles and exploring the connections to other mathematical concepts will significantly enhance your problem-solving abilities. The example of finding the LCM of 3, 9, and 15 provides a solid foundation for tackling more complex LCM problems in the future. Remember to choose the method most suitable for the specific numbers and context of the problem.
Latest Posts
Related Post
Thank you for visiting our website which covers about Least Common Multiple Of 3 9 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.