Least Common Multiple Of 4 5 And 6
News Co
Apr 06, 2025 · 5 min read
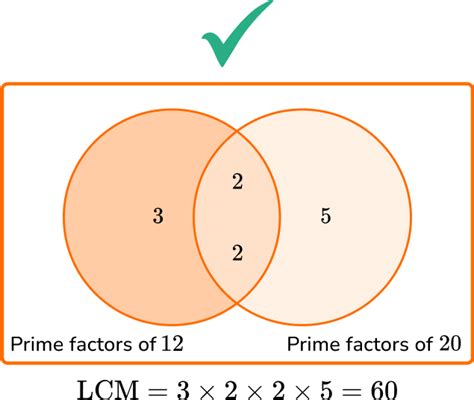
Table of Contents
Finding the Least Common Multiple (LCM) of 4, 5, and 6: A Comprehensive Guide
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts and various methods for calculating it can be incredibly valuable, particularly in areas like scheduling, measurement conversions, and even music theory. This article dives deep into determining the LCM of 4, 5, and 6, exploring multiple approaches and illustrating the practical applications of this fundamental mathematical concept.
Understanding Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. In simpler terms, it's the smallest number that all the given numbers can divide into evenly. This contrasts with the greatest common divisor (GCD), which is the largest number that divides all the given numbers without leaving a remainder. Understanding the difference between LCM and GCD is crucial for mastering this area of mathematics.
For example, let's consider the numbers 2 and 3. Multiples of 2 are 2, 4, 6, 8, 10, 12... and multiples of 3 are 3, 6, 9, 12, 15... The smallest number that appears in both lists is 6, making 6 the LCM of 2 and 3.
Methods for Calculating LCM
Several methods exist for calculating the LCM, each with its own advantages and disadvantages. Let's explore the most common approaches, focusing on their application to find the LCM of 4, 5, and 6.
1. Listing Multiples Method
This is the most straightforward method, particularly useful for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60...
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60...
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60...
By inspecting the lists, we can see that the smallest number appearing in all three lists is 60. Therefore, the LCM of 4, 5, and 6 is 60. This method is simple but can become time-consuming and impractical for larger numbers.
2. Prime Factorization Method
This method is more efficient for larger numbers. We find the prime factorization of each number and then construct the LCM using the highest powers of each prime factor.
- Prime factorization of 4: 2²
- Prime factorization of 5: 5¹
- Prime factorization of 6: 2¹ × 3¹
To find the LCM, we take the highest power of each prime factor present in the factorizations:
- Highest power of 2: 2² = 4
- Highest power of 3: 3¹ = 3
- Highest power of 5: 5¹ = 5
Now, multiply these highest powers together: 4 × 3 × 5 = 60. Therefore, the LCM of 4, 5, and 6 is 60. This method is generally more efficient than listing multiples, especially when dealing with larger numbers.
3. Greatest Common Divisor (GCD) Method
The LCM and GCD are related through the following formula:
LCM(a, b) × GCD(a, b) = a × b
This relationship holds true for any two numbers a and b. We can extend this to multiple numbers, but it requires iterative calculations. First, find the GCD of any two numbers, then find the LCM of that result and the third number, and so on.
Let's use the Euclidean algorithm to find the GCD of 4 and 6:
- 6 = 1 × 4 + 2
- 4 = 2 × 2 + 0
The GCD of 4 and 6 is 2.
Now, let's use the formula LCM(a, b) = (a × b) / GCD(a, b) to find the LCM of 4 and 6:
LCM(4, 6) = (4 × 6) / 2 = 12
Finally, we find the LCM of 12 and 5:
LCM(12, 5) = (12 × 5) / GCD(12, 5) = (12 × 5) / 1 = 60 (The GCD of 12 and 5 is 1).
Therefore, the LCM of 4, 5, and 6 is 60. This method is less intuitive for larger sets of numbers but demonstrates the important relationship between LCM and GCD.
Practical Applications of LCM
The LCM has various applications across different fields:
1. Scheduling Problems
Imagine you have three machines that perform different tasks. Machine A completes its cycle every 4 hours, Machine B every 5 hours, and Machine C every 6 hours. To determine when all three machines will complete their cycles simultaneously, you need to find the LCM of 4, 5, and 6, which is 60. All three machines will complete their cycles together after 60 hours.
2. Measurement Conversions
Converting between different units of measurement often involves finding the LCM. For example, converting fractions to a common denominator requires finding the LCM of the denominators.
3. Music Theory
In music, the LCM is used to determine the least common period of two or more musical phrases with different rhythmic patterns. This helps in understanding and composing complex musical structures.
4. Project Management
In project scheduling, the LCM can be utilized to synchronize various tasks with different durations, allowing for optimal resource allocation and timely completion.
Conclusion: Mastering LCM Calculations
The calculation of the least common multiple (LCM) is a fundamental arithmetic skill with widespread applications. Whether you're tackling scheduling problems, converting measurements, or exploring musical rhythms, understanding the LCM and mastering the various methods for calculating it are crucial for efficiency and accuracy. While the listing multiples method is suitable for small numbers, the prime factorization method is generally more efficient for larger numbers. Understanding the relationship between LCM and GCD provides an alternative calculation method, particularly beneficial when dealing with more complex scenarios. The ability to efficiently calculate the LCM contributes significantly to problem-solving across multiple disciplines. By grasping the concept and applying the right method, you can confidently navigate the world of multiples and divisors.
Latest Posts
Related Post
Thank you for visiting our website which covers about Least Common Multiple Of 4 5 And 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.