Least Common Multiple Of 6 7 And 8
News Co
Apr 04, 2025 · 5 min read
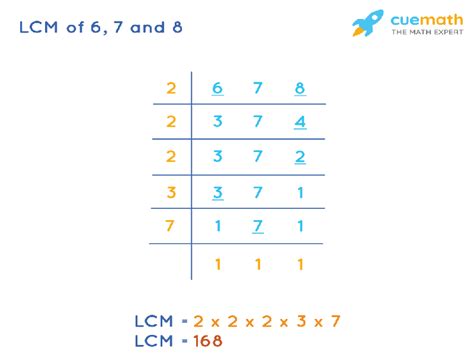
Table of Contents
Finding the Least Common Multiple (LCM) of 6, 7, and 8: A Comprehensive Guide
The least common multiple (LCM) is a fundamental concept in mathematics with widespread applications in various fields, from scheduling problems to music theory. This article provides a comprehensive guide to finding the LCM of 6, 7, and 8, exploring different methods and delving into the underlying mathematical principles. We'll also explore the practical applications and significance of understanding LCMs.
Understanding Least Common Multiples
Before diving into the calculation, let's solidify our understanding of what an LCM actually is. The least common multiple of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly.
Key Concepts:
- Multiple: A multiple of a number is the result of multiplying that number by any integer (e.g., multiples of 6 are 6, 12, 18, 24, etc.).
- Common Multiple: A common multiple of two or more numbers is a number that is a multiple of all the numbers. For example, common multiples of 6 and 8 are 24, 48, 72, and so on.
- Least Common Multiple (LCM): The smallest of these common multiples is the LCM.
Methods for Finding the LCM of 6, 7, and 8
There are several methods to determine the LCM of 6, 7, and 8. We will explore three common approaches:
1. Listing Multiples Method
This method, while straightforward, can be time-consuming for larger numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78, 84, 90, 96, 102, 108, 114, 120, ...
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98, 105, 112, 119, 126, 133, 140, ...
- Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96, 104, 112, 120, 128, 136, 144, 152, 160,...
By comparing the lists, we can see that the smallest number appearing in all three lists is 168. Therefore, the LCM of 6, 7, and 8 is 168.
2. Prime Factorization Method
This method is generally more efficient, especially for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM from the prime factors.
- Prime factorization of 6: 2 x 3
- Prime factorization of 7: 7 (7 is a prime number)
- Prime factorization of 8: 2 x 2 x 2 = 2³
To find the LCM, we take the highest power of each prime factor present in the factorizations:
- The highest power of 2 is 2³ = 8
- The highest power of 3 is 3¹ = 3
- The highest power of 7 is 7¹ = 7
Multiplying these together: 8 x 3 x 7 = 168. Therefore, the LCM of 6, 7, and 8 is 168.
3. Greatest Common Divisor (GCD) Method
This method utilizes the relationship between the LCM and the greatest common divisor (GCD) of two numbers. The LCM and GCD of two numbers (a and b) are related by the formula: LCM(a, b) x GCD(a, b) = a x b. However, extending this directly to three numbers requires a more iterative approach. We can find the LCM of 6 and 7 first, and then find the LCM of that result and 8.
- LCM(6, 7): Since 6 and 7 are relatively prime (their GCD is 1), their LCM is simply their product: 6 x 7 = 42.
- LCM(42, 8): We can use prime factorization:
- 42 = 2 x 3 x 7
- 8 = 2³
- LCM(42, 8) = 2³ x 3 x 7 = 8 x 3 x 7 = 168
Therefore, the LCM of 6, 7, and 8 is 168.
Why is Finding the LCM Important?
Understanding and calculating the LCM has numerous practical applications across various fields:
1. Scheduling and Timing Problems
Imagine you have three different machines that complete a cycle in 6, 7, and 8 hours respectively. To find out when all three machines will complete a cycle simultaneously, you need to find the LCM of 6, 7, and 8. The LCM, 168, indicates that all three machines will complete a cycle together after 168 hours.
2. Fraction Operations
When adding or subtracting fractions with different denominators, finding the LCM of the denominators is crucial to finding a common denominator. This simplifies the process of performing the addition or subtraction.
3. Music Theory
LCMs play a role in music theory, particularly in determining the least common multiple of the note values. This helps in understanding rhythmic patterns and harmonies.
4. Gear Ratios and Mechanical Engineering
In mechanical engineering, LCMs can be used to calculate gear ratios and synchronize the rotations of different gears within a system.
Advanced Techniques and Considerations
For larger sets of numbers or when dealing with more complex scenarios, more advanced techniques such as the Euclidean algorithm (for finding the GCD) and specialized algorithms for computing LCMs efficiently become necessary. These algorithms are often implemented in computer programs to handle calculations for very large numbers.
Conclusion
Finding the least common multiple of 6, 7, and 8, as demonstrated through various methods, highlights the importance of this fundamental mathematical concept. The ability to calculate the LCM is not just a theoretical exercise; it's a practical skill with broad applications in diverse fields. Mastering different methods for calculating the LCM allows for efficient problem-solving across a range of contexts, from basic arithmetic to advanced engineering applications. Understanding the underlying principles and applying appropriate methods ensures accurate and efficient results, leading to a stronger grasp of mathematical concepts and problem-solving skills.
Latest Posts
Related Post
Thank you for visiting our website which covers about Least Common Multiple Of 6 7 And 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.