Least Common Multiple Of 7 And 2
News Co
Mar 28, 2025 · 5 min read
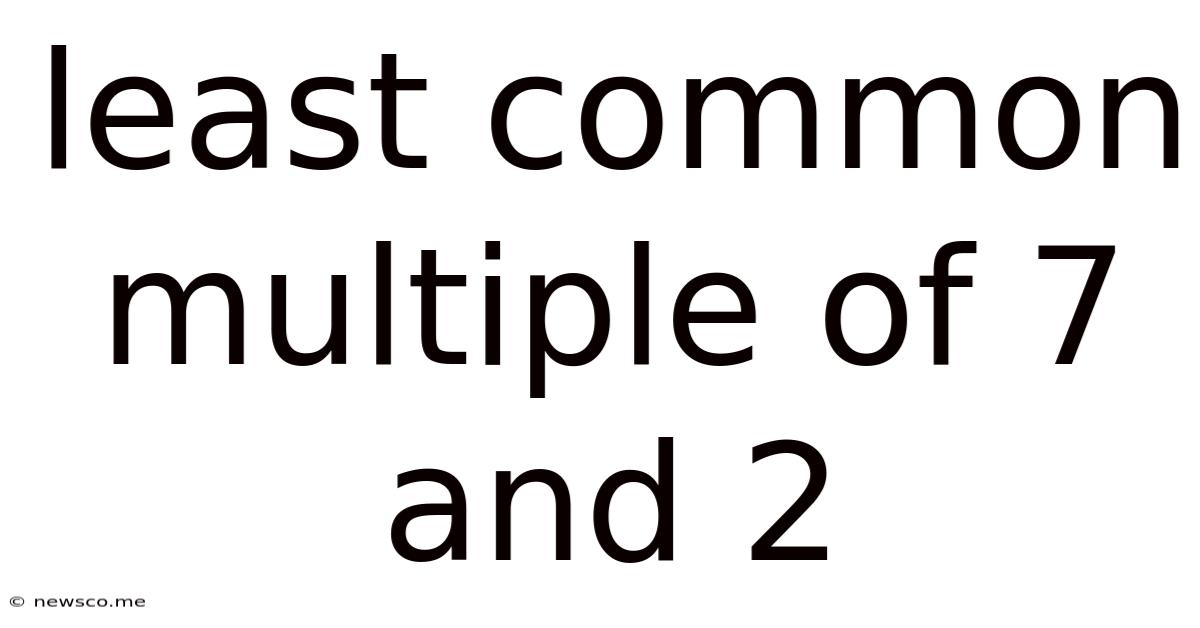
Table of Contents
Finding the Least Common Multiple (LCM) of 7 and 2: A Comprehensive Guide
The least common multiple (LCM) is a fundamental concept in mathematics, particularly in number theory and arithmetic. Understanding how to find the LCM is crucial for various applications, from simplifying fractions to solving problems in algebra and beyond. This article provides a comprehensive guide to calculating the LCM of 7 and 2, explaining the underlying principles and showcasing multiple methods to arrive at the solution. We’ll explore both manual calculation techniques and the use of prime factorization, making this a resource valuable for students and anyone looking to refresh their mathematical skills.
What is the Least Common Multiple (LCM)?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that is a multiple of each of the given numbers. For instance, the LCM of 2 and 3 is 6 because 6 is the smallest positive integer that is divisible by both 2 and 3.
Finding the LCM is essential in many mathematical contexts, including:
- Simplifying fractions: Determining the LCM of the denominators allows for easy addition and subtraction of fractions.
- Solving equations: LCM is used in solving equations involving fractions and rational expressions.
- Scheduling problems: LCM helps determine when events with different periodicities will coincide (e.g., when two buses with different schedules will arrive at a stop simultaneously).
- Rhythm and music: LCM is used in music to find the least common denominator of different rhythmic patterns.
Methods for Finding the LCM of 7 and 2
There are several methods to calculate the LCM of two numbers, particularly small ones like 7 and 2. Let's explore the most common approaches:
1. Listing Multiples Method
This is a straightforward method, especially effective for small numbers. We list the multiples of each number until we find the smallest multiple common to both.
- Multiples of 7: 7, 14, 21, 28, 35, 42...
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16...
Observing the lists, the smallest multiple present in both sequences is 14. Therefore, the LCM of 7 and 2 is 14.
2. Prime Factorization Method
This method is more systematic and works well for larger numbers or when dealing with multiple numbers simultaneously. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor.
- Prime Factorization of 7: 7 (7 is a prime number, meaning its only divisors are 1 and itself)
- Prime Factorization of 2: 2 (2 is also a prime number)
Since 7 and 2 are both prime and distinct, the LCM is simply their product: 7 x 2 = 14.
3. Using the Formula: LCM(a, b) = (|a x b|) / GCD(a, b)
This method uses the greatest common divisor (GCD) of the two numbers. The GCD is the largest positive integer that divides both numbers without leaving a remainder. We can then use the formula: LCM(a, b) = (|a x b|) / GCD(a, b)
- Finding the GCD of 7 and 2: The GCD of 7 and 2 is 1 because 1 is the only positive integer that divides both 7 and 2.
- Applying the formula: LCM(7, 2) = (7 x 2) / 1 = 14
This method is particularly useful for larger numbers where finding the prime factorization might be more tedious. The GCD can be found using the Euclidean algorithm, a relatively efficient method for larger numbers.
Why is Understanding LCM Important?
The concept of LCM extends far beyond simple calculations. It's a foundational concept with wide-ranging applications in various fields:
-
Fraction Arithmetic: Adding or subtracting fractions requires a common denominator. The LCM of the denominators provides the least common denominator (LCD), simplifying the process. For example, adding 1/7 and 1/2 requires finding the LCM of 7 and 2, which is 14. Then, we can rewrite the fractions as 2/14 and 7/14 respectively, making addition straightforward.
-
Modular Arithmetic: LCM plays a crucial role in modular arithmetic, which deals with remainders after division. This has applications in cryptography and computer science.
-
Scheduling and Synchronization: Imagine two machines operating on different cycles. The LCM helps determine when they will both be at a specific point in their cycles simultaneously. This has applications in manufacturing, logistics, and scheduling events.
-
Music Theory: Rhythmic patterns in music are often represented using fractions. The LCM helps determine the least common denominator of these fractions, facilitating synchronization of different rhythmic elements within a piece of music.
-
Real-world problem solving: Many real-world problems involve finding the smallest common multiple of different quantities or cycles. This could include anything from optimizing production lines to planning events that occur at different intervals.
Extending the Concept: LCM of More Than Two Numbers
The methods discussed above can be extended to find the LCM of more than two numbers. The prime factorization method is generally the most efficient for this case. You find the prime factorization of each number, then construct the LCM by taking the highest power of each prime factor present in any of the factorizations.
For example, to find the LCM of 2, 3, and 6:
- Prime factorization of 2: 2
- Prime factorization of 3: 3
- Prime factorization of 6: 2 x 3
The LCM is 2 x 3 = 6. The highest power of 2 is 2¹ and the highest power of 3 is 3¹.
Conclusion: Mastering the LCM
The least common multiple is a powerful tool with broad applications across various mathematical disciplines and real-world scenarios. Understanding how to calculate the LCM using different methods, from simple listing to prime factorization and the GCD-based formula, equips you with a valuable skill. Whether you're simplifying fractions, solving equations, or tackling more complex problems, a firm grasp of the LCM will significantly enhance your mathematical abilities and problem-solving skills. Remember that practice is key to mastering this concept, so try working through various examples to solidify your understanding. The more you practice, the more intuitive and efficient you will become at calculating the LCM of any set of numbers.
Latest Posts
Related Post
Thank you for visiting our website which covers about Least Common Multiple Of 7 And 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.