Least Common Multiple Of 8 12 15
News Co
Apr 12, 2025 · 5 min read
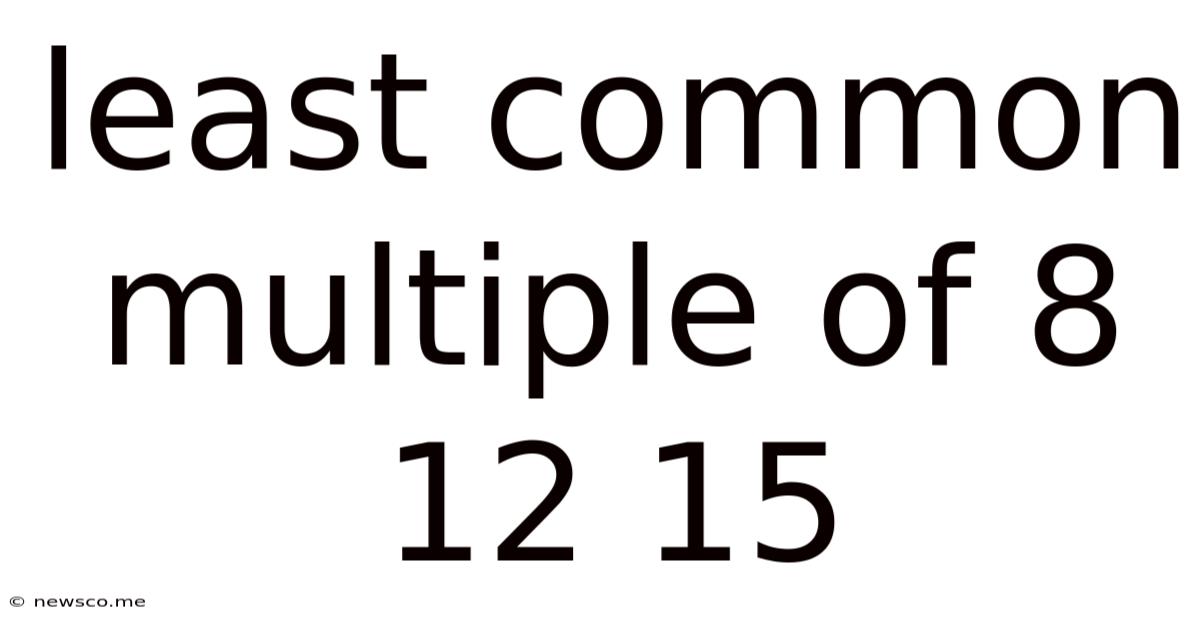
Table of Contents
Finding the Least Common Multiple (LCM) of 8, 12, and 15: A Comprehensive Guide
The least common multiple (LCM) is a fundamental concept in mathematics with wide-ranging applications, from simplifying fractions to solving complex scheduling problems. This article will delve deep into the process of calculating the LCM of 8, 12, and 15, exploring different methods and providing a comprehensive understanding of the underlying principles. We'll also touch upon the broader significance of LCM in various fields.
Understanding Least Common Multiple (LCM)
Before we dive into calculating the LCM of 8, 12, and 15, let's solidify our understanding of the concept itself. The least common multiple of two or more numbers is the smallest positive integer that is a multiple of all the numbers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly without leaving a remainder.
For example, let's consider the numbers 2 and 3. The multiples of 2 are 2, 4, 6, 8, 10, 12, and so on. The multiples of 3 are 3, 6, 9, 12, 15, and so on. The common multiples of 2 and 3 are 6, 12, 18, and so on. The smallest of these common multiples is 6, therefore, the LCM of 2 and 3 is 6.
Method 1: Listing Multiples
One straightforward method for finding the LCM is by listing the multiples of each number until a common multiple is found. While this method works well for smaller numbers, it becomes less efficient as the numbers increase in size.
Let's apply this method to find the LCM of 8, 12, and 15:
- Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96, 104, 112, 120...
- Multiples of 12: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120...
- Multiples of 15: 15, 30, 45, 60, 75, 90, 105, 120...
By comparing the lists, we can see that the smallest common multiple of 8, 12, and 15 is 120. Therefore, the LCM(8, 12, 15) = 120.
Method 2: Prime Factorization
A more efficient and systematic method for finding the LCM involves prime factorization. This method is particularly useful when dealing with larger numbers. Prime factorization involves expressing each number as a product of its prime factors.
Let's find the prime factorization of 8, 12, and 15:
- 8 = 2 x 2 x 2 = 2³
- 12 = 2 x 2 x 3 = 2² x 3
- 15 = 3 x 5
To find the LCM using prime factorization, we identify the highest power of each prime factor present in the factorizations:
- The highest power of 2 is 2³ = 8
- The highest power of 3 is 3¹ = 3
- The highest power of 5 is 5¹ = 5
Now, multiply these highest powers together:
LCM(8, 12, 15) = 2³ x 3 x 5 = 8 x 3 x 5 = 120
This method confirms our result from the listing multiples method.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) are closely related. The product of the LCM and GCD of two numbers is equal to the product of the two numbers. This relationship can be extended to more than two numbers, although the calculation becomes more complex.
First, let's find the GCD of 8, 12, and 15 using the Euclidean algorithm or prime factorization. The GCD(8, 12, 15) = 1. (They share no common factors other than 1).
While the direct application of this relationship to three numbers is less straightforward, it highlights the interconnectedness of LCM and GCD.
Real-World Applications of LCM
The concept of LCM extends beyond abstract mathematical exercises. It has practical applications in various fields:
-
Scheduling: Imagine you have three machines that cycle at different intervals: Machine A every 8 hours, Machine B every 12 hours, and Machine C every 15 hours. To find when all three machines will complete a cycle simultaneously, you need to find the LCM(8, 12, 15) = 120 hours. This is the time when all machines will be at their starting point again.
-
Fraction Operations: Finding the LCM of denominators is crucial when adding or subtracting fractions. It allows you to find a common denominator, simplifying the calculations.
-
Music Theory: LCM plays a role in determining the least common period of musical rhythms.
-
Gear Ratios: In mechanical engineering, LCM helps to calculate gear ratios and synchronize rotational speeds.
-
Project Management: In project management, LCM can help in scheduling tasks that depend on each other, ensuring efficient resource utilization.
Expanding on the Prime Factorization Method
The prime factorization method remains the most robust and efficient way to calculate the LCM, especially for larger numbers or a greater number of integers. Let's consider a more complex example to illustrate its power:
Find the LCM of 24, 36, and 60.
-
Prime Factorization:
- 24 = 2³ x 3
- 36 = 2² x 3²
- 60 = 2² x 3 x 5
-
Identifying Highest Powers:
- Highest power of 2: 2³ = 8
- Highest power of 3: 3² = 9
- Highest power of 5: 5¹ = 5
-
Calculating the LCM:
- LCM(24, 36, 60) = 2³ x 3² x 5 = 8 x 9 x 5 = 360
Therefore, the least common multiple of 24, 36, and 60 is 360. This demonstrates how the prime factorization method simplifies the calculation even with larger numbers.
Advanced Considerations and Further Exploration
While the methods described above cover the core concepts, exploring further mathematical concepts can enhance understanding and efficiency.
-
Euclidean Algorithm for GCD: The Euclidean algorithm provides an efficient way to calculate the GCD of two numbers, which can then be used in conjunction with the LCM formula.
-
Modular Arithmetic: Understanding modular arithmetic can provide alternative approaches to solving LCM problems within specific contexts.
-
Computational Algorithms: For very large numbers, sophisticated computational algorithms exist to efficiently compute LCMs, employing optimized data structures and techniques.
Conclusion
Finding the least common multiple, while seemingly a simple mathematical operation, underpins many practical applications across diverse fields. Understanding the different methods for calculating the LCM, particularly the prime factorization method, is essential for solving various mathematical and real-world problems. This comprehensive guide has not only shown you how to calculate the LCM of 8, 12, and 15 but has also equipped you with the knowledge to tackle similar problems with greater confidence and efficiency. Remember to choose the method best suited to the numbers involved, recognizing the strengths and limitations of each approach. Continued exploration of related mathematical concepts will only deepen your understanding and broaden the scope of your problem-solving abilities.
Latest Posts
Related Post
Thank you for visiting our website which covers about Least Common Multiple Of 8 12 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.