Least Common Multiple Of 8 And 2
News Co
Apr 03, 2025 · 5 min read
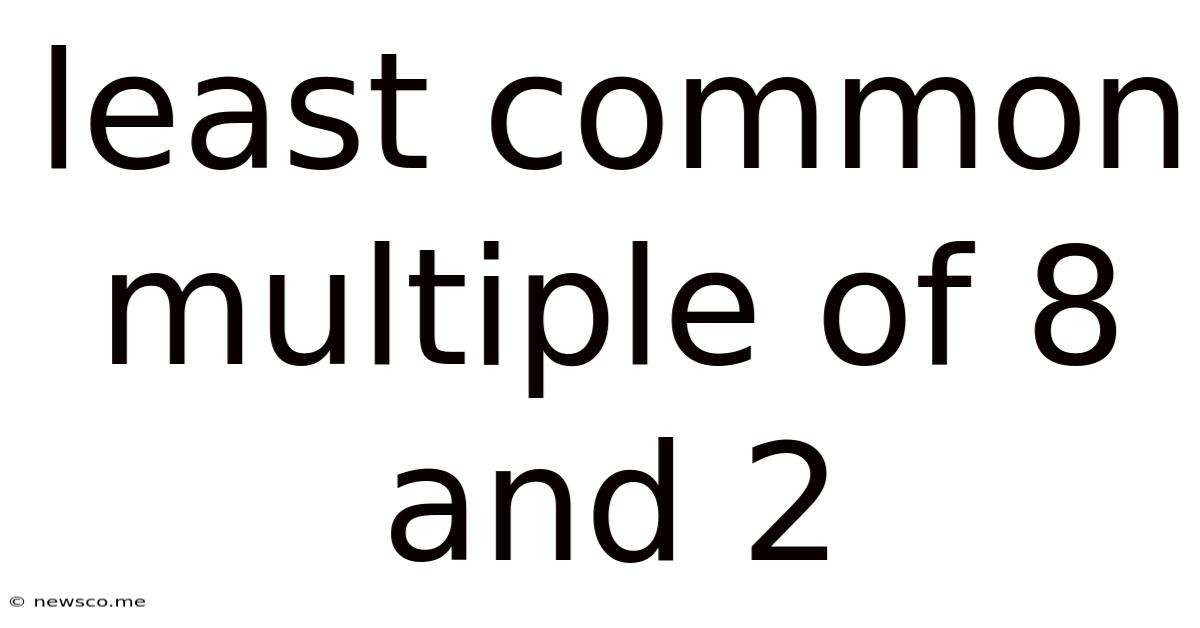
Table of Contents
Unveiling the Least Common Multiple (LCM) of 8 and 2: A Deep Dive
Finding the least common multiple (LCM) might seem like a simple arithmetic task, especially when dealing with small numbers like 8 and 2. However, understanding the underlying concepts and exploring different methods for calculating the LCM provides valuable insights into number theory and its applications in various fields, from scheduling problems to musical harmony. This article will delve deep into the LCM of 8 and 2, exploring multiple approaches and highlighting their significance.
Understanding Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. It's a fundamental concept in number theory with far-reaching applications. Think of it as the smallest number that contains all the prime factors of the given numbers, each raised to the highest power it appears in any of the numbers.
Importance of LCM
The LCM isn't just a mathematical curiosity; it has practical applications in diverse areas:
- Scheduling: Determining the time when two events coincide. For instance, if two buses arrive at a stop every 8 minutes and 2 minutes, respectively, the LCM helps determine when they'll arrive simultaneously.
- Music Theory: Harmonizing musical intervals and creating rhythmic patterns. The LCM ensures that musical phrases align seamlessly.
- Fractions: Finding a common denominator when adding or subtracting fractions is fundamentally based on the LCM.
- Project Management: Synchronizing tasks with different completion times.
Calculating the LCM of 8 and 2: Multiple Methods
Let's explore several methods to calculate the LCM of 8 and 2. While the numbers are simple, understanding these methods is crucial for tackling more complex scenarios.
Method 1: Listing Multiples
This method is straightforward, especially for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 8: 8, 16, 24, 32, 40, ...
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, ...
The smallest multiple that appears in both lists is 8. Therefore, the LCM(8, 2) = 8.
Method 2: Prime Factorization
This is a more powerful method that works effectively for larger numbers and helps illustrate the underlying structure of the LCM.
- Prime Factorization of 8: 2 x 2 x 2 = 2³
- Prime Factorization of 2: 2
To find the LCM, we take the highest power of each prime factor present in either number. In this case, the only prime factor is 2, and its highest power is 2³.
Therefore, LCM(8, 2) = 2³ = 8.
Method 3: Using the Formula LCM(a, b) = (|a x b|) / GCD(a, b)
This method involves the greatest common divisor (GCD). The GCD of two numbers is the largest number that divides both without leaving a remainder.
- GCD(8, 2): The GCD of 8 and 2 is 2.
- Applying the Formula: LCM(8, 2) = (8 x 2) / 2 = 8
This formula provides a concise and efficient way to calculate the LCM, especially for larger numbers where listing multiples might be impractical.
Deep Dive into Prime Factorization and its Relation to LCM
Prime factorization is the cornerstone of understanding LCM. Let's delve deeper into why it works so effectively.
Every integer greater than 1 can be uniquely expressed as a product of prime numbers. This fundamental theorem of arithmetic forms the basis for numerous mathematical concepts. When we find the prime factorization of two numbers, we essentially break them down into their fundamental building blocks.
The LCM, in essence, constructs the smallest number that contains all these building blocks (prime factors) with the highest power they appear in either of the original numbers. This ensures that the LCM is divisible by both numbers.
For example:
Let's find the LCM of 12 and 18.
- Prime factorization of 12: 2² x 3
- Prime factorization of 18: 2 x 3²
The LCM will include the highest power of each prime factor present: 2² and 3².
Therefore, LCM(12, 18) = 2² x 3² = 4 x 9 = 36.
Applications of LCM: Real-World Examples
The LCM finds applications in diverse real-world scenarios, illustrating its practical importance beyond theoretical mathematics.
Scheduling and Synchronization
Imagine two machines in a factory operating on different cycles. One completes a cycle every 8 hours, and the other every 2 hours. To schedule maintenance simultaneously for both, we need to find the LCM(8, 2), which is 8. Maintenance can be scheduled every 8 hours to ensure both machines are down simultaneously.
Music and Rhythm
In music, the LCM helps create rhythmic patterns and harmonious intervals. If a musical phrase repeats every 8 beats and another every 2 beats, they'll perfectly align every 8 beats (LCM(8, 2) = 8). This ensures a pleasing and coherent musical structure.
Working with Fractions
Adding or subtracting fractions requires a common denominator. The LCM of the denominators serves as the least common denominator (LCD), simplifying the calculations. For example, to add 1/8 and 1/2, we find the LCM(8, 2) = 8, making 8 the LCD.
Extending the Concept: LCM of More Than Two Numbers
The concepts discussed extend seamlessly to finding the LCM of more than two numbers. The prime factorization method remains particularly efficient. We simply find the prime factorization of each number and include the highest power of each prime factor present in any of the numbers.
For instance, to find LCM(4, 6, 10):
- Prime factorization of 4: 2²
- Prime factorization of 6: 2 x 3
- Prime factorization of 10: 2 x 5
The highest powers are 2², 3, and 5.
Therefore, LCM(4, 6, 10) = 2² x 3 x 5 = 60.
Conclusion: The Ubiquitous LCM
The seemingly simple concept of the least common multiple extends far beyond basic arithmetic. Its applications in scheduling, music theory, fraction arithmetic, and beyond demonstrate its practical value. Understanding different methods for calculating the LCM, especially the prime factorization method, provides a powerful tool for solving diverse problems across numerous disciplines. The next time you encounter a problem involving synchronization, rhythm, or fraction addition, remember the power and versatility of the least common multiple. It's a fundamental concept with far-reaching implications, proving that even seemingly simple mathematical ideas can have a profound impact on our understanding and interaction with the world around us.
Latest Posts
Related Post
Thank you for visiting our website which covers about Least Common Multiple Of 8 And 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.