Length Times Width Times Height Equals
News Co
Mar 25, 2025 · 6 min read
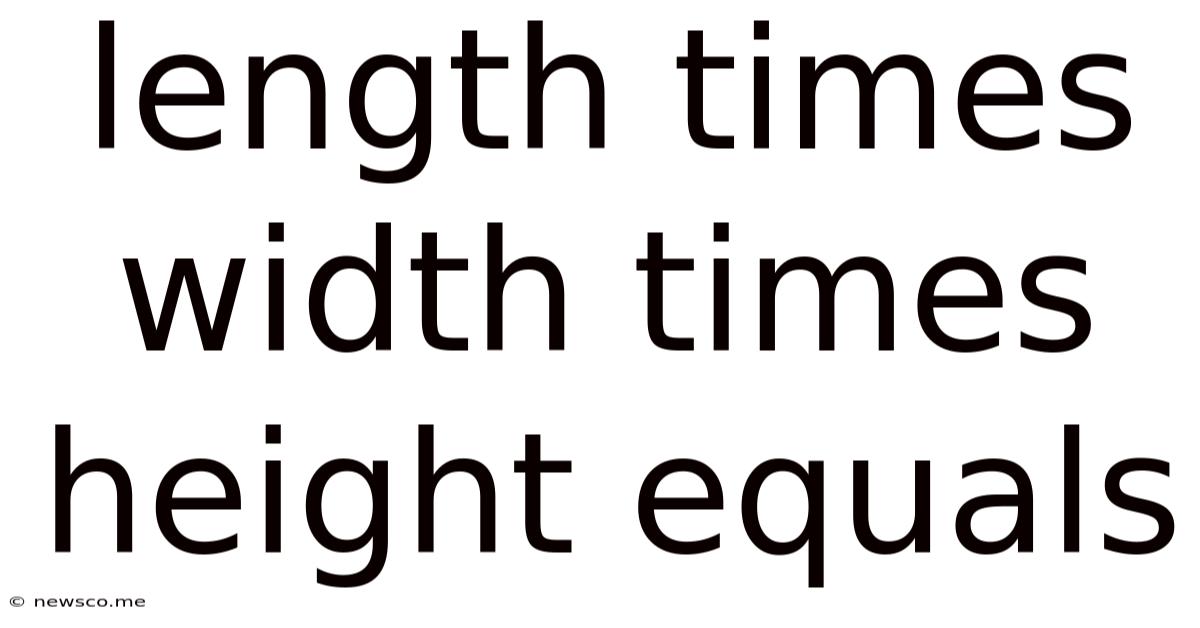
Table of Contents
Length Times Width Times Height Equals: A Deep Dive into Volume Calculation
Understanding the formula "length times width times height equals volume" is fundamental to numerous fields, from everyday tasks to advanced engineering projects. This seemingly simple equation unlocks the ability to calculate the space occupied by three-dimensional objects, impacting everything from package delivery to architectural design. This comprehensive guide delves into the intricacies of this formula, exploring its applications, variations, and the importance of accurate measurement.
Understanding the Basics: Volume and its Calculation
The core concept revolves around volume, which represents the amount of three-dimensional space occupied by an object or substance. Think of it as the quantity of space enclosed within a given boundary. For objects with regular shapes – like cubes, rectangular prisms, and cuboids – calculating volume is straightforward. The fundamental formula for this calculation is:
Volume = Length × Width × Height
This equation holds true for any rectangular prism or cuboid. A cuboid is simply a three-dimensional shape with six rectangular faces. A cube, a special case of a cuboid, has all sides of equal length. In a cube, the formula simplifies to:
Volume = Side × Side × Side = Side³
Defining Length, Width, and Height
Before diving into calculations, it’s crucial to understand what constitutes length, width, and height. These terms represent the three spatial dimensions of the object:
- Length: Typically, the longest dimension of the object. Think of it as the extent from one end to the other.
- Width: The dimension perpendicular to the length, often the shorter dimension across the face of the object.
- Height: The dimension perpendicular to both length and width, representing the vertical extent of the object.
It’s important to note that these labels are somewhat arbitrary. You could rotate the object and relabel the dimensions, but the resulting volume will always be the same. The key is to measure the three perpendicular dimensions accurately.
Practical Applications: Where Volume Calculation Matters
The seemingly simple equation, "length times width times height equals volume," finds applications across a wide spectrum of fields:
1. Packaging and Shipping
Calculating the volume of packages is essential for shipping and logistics. Companies must determine the dimensions of packages to optimize space in trucks, containers, and warehouses. Accurate volume calculations minimize wasted space and reduce shipping costs. Incorrect estimations can lead to inefficient packing and increased shipping expenses.
2. Construction and Engineering
Architects and engineers rely heavily on volume calculations in designing buildings, bridges, and other structures. Determining the volume of materials required, such as concrete or steel, is crucial for accurate budgeting and efficient construction. This applies equally to smaller-scale projects like building a deck or a shed.
3. Agriculture and Farming
In agriculture, understanding volume is critical for tasks such as determining the amount of fertilizer needed for a field or the capacity of a grain silo. Accurate volume calculations ensure efficient resource management and optimize yields.
4. Medicine and Healthcare
In medicine, accurate volume calculations are crucial for dispensing medication, determining blood volume, and calculating the dosage of intravenous fluids. Precision in these calculations is vital for patient safety and effective treatment.
5. Manufacturing and Production
Manufacturers rely on volume calculations to optimize product design, determine material usage, and calculate the capacity of storage tanks. Accurate volume calculations streamline production processes and minimize waste.
6. Environmental Science
Environmental scientists use volume calculations to measure the capacity of lakes, reservoirs, and aquifers. These measurements are vital for water resource management and environmental impact assessments.
Beyond Rectangular Prisms: Dealing with Irregular Shapes
While the length × width × height formula works perfectly for rectangular prisms, many objects have irregular shapes. Calculating the volume of irregular shapes requires more sophisticated methods:
1. Water Displacement Method
This simple yet effective method involves submerging the object in a container of water and measuring the volume of water displaced. The volume of the displaced water is equal to the volume of the object.
2. Numerical Integration
For complex shapes, numerical integration techniques can be employed. These methods involve breaking down the irregular shape into smaller, simpler shapes and summing their volumes.
3. 3D Scanning and Modeling
Advanced techniques like 3D scanning create a digital model of the object, allowing for precise volume calculations using specialized software.
The Importance of Accurate Measurement
The accuracy of volume calculations depends heavily on the accuracy of the measurements of length, width, and height. Inaccurate measurements lead to incorrect volume calculations, resulting in errors in various applications. Therefore, employing appropriate measuring tools and techniques is vital:
1. Choosing the Right Measuring Tools
Select tools appropriate for the size and shape of the object. For smaller objects, rulers or calipers might suffice, while larger objects may require measuring tapes or laser distance meters.
2. Employing Proper Measuring Techniques
Ensure measurements are taken perpendicular to each other. Multiple measurements should be taken and averaged to minimize errors.
3. Using Appropriate Units
Consistency in units is paramount. All measurements must be in the same unit (e.g., centimeters, meters, inches) to ensure accurate calculations.
Units of Volume: A Quick Overview
The units used to express volume depend on the context and the system of measurement:
- Cubic meters (m³): The standard unit in the International System of Units (SI).
- Cubic centimeters (cm³): Commonly used for smaller volumes.
- Liters (L): A metric unit of volume equivalent to 1000 cm³.
- Cubic feet (ft³): Commonly used in the imperial system.
- Cubic inches (in³): Used for smaller volumes in the imperial system.
- Gallons (gal): A unit of volume in the imperial system, commonly used for liquids.
It's crucial to convert units when necessary to ensure consistent calculations.
Troubleshooting Common Errors in Volume Calculations
Several common errors can occur when calculating volume:
- Incorrect Measurement Units: Using inconsistent units (e.g., mixing centimeters and meters) will lead to incorrect results.
- Improper Measurement Techniques: Failing to measure perpendicular dimensions or neglecting to take multiple measurements can introduce significant errors.
- Incorrect Formula Application: Using the wrong formula for irregularly shaped objects will lead to inaccurate volume estimations.
- Rounding Errors: Rounding off measurements too early in the calculation can accumulate errors.
Careful attention to detail and the use of appropriate tools and techniques will minimize these errors.
Conclusion: The Power of a Simple Equation
The seemingly simple equation, "length times width times height equals volume," holds immense practical significance. From everyday tasks to complex engineering projects, accurately calculating volume is crucial for efficiency, accuracy, and safety. Understanding the fundamentals of this formula, along with the importance of accurate measurements and appropriate units, empowers individuals and professionals across various fields to make informed decisions and optimize processes. By mastering this equation, you unlock a world of possibilities in understanding and interacting with the three-dimensional world around us.
Latest Posts
Related Post
Thank you for visiting our website which covers about Length Times Width Times Height Equals . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.