Less Than Or Equal To Sign On Number Line
News Co
May 08, 2025 · 6 min read
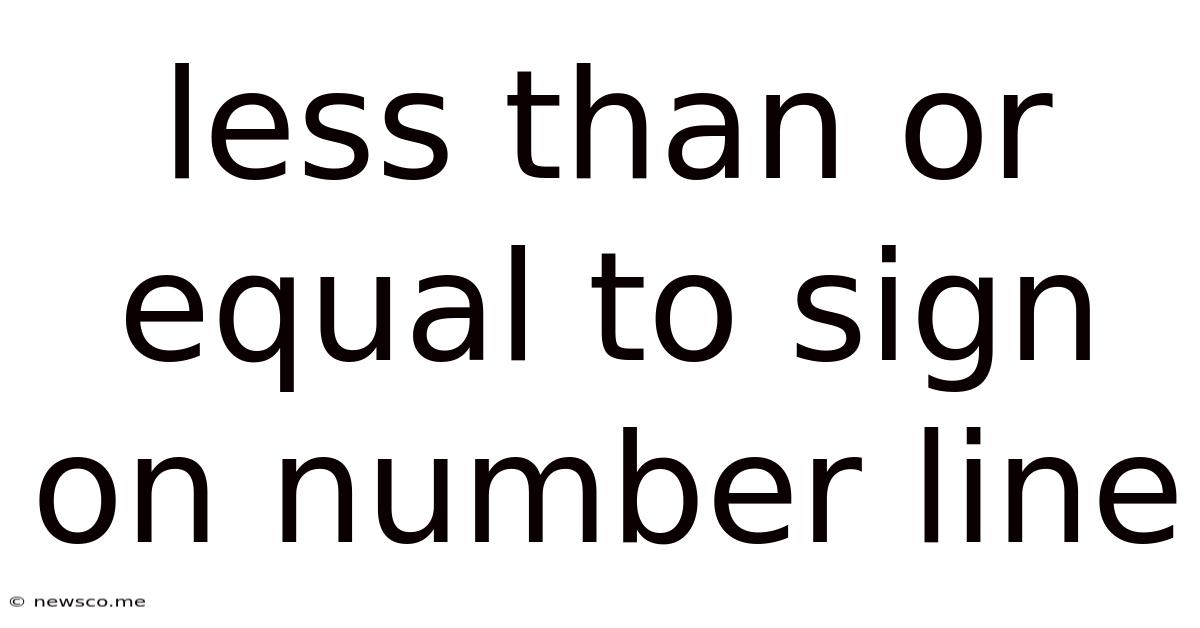
Table of Contents
Less Than or Equal To Sign on a Number Line: A Comprehensive Guide
Understanding mathematical symbols and their graphical representations is crucial for grasping fundamental concepts and solving various problems. This comprehensive guide delves into the meaning and application of the "less than or equal to" sign (≤) on a number line. We will explore its significance in number theory, algebra, and beyond, providing practical examples and visualizations to solidify your understanding.
What Does ≤ Mean?
The "less than or equal to" sign (≤) is a mathematical symbol used to represent a relationship between two values. It indicates that the value on the left side of the symbol is either less than or equal to the value on the right side. In simpler terms, it combines the concepts of "less than" (<) and "equal to" (=).
Key takeaway: a ≤ b means that 'a' is less than or equal to 'b'. This holds true if a is less than b, or if a is equal to b.
Representing ≤ on a Number Line
A number line provides a visual representation of numbers, ordered from least to greatest. Representing "less than or equal to" on a number line involves shading the region encompassing all values satisfying the inequality.
Simple Inequalities
Let's consider a simple inequality: x ≤ 3. This means x can be any number less than 3, or it can be equal to 3. On the number line:
- Locate the number 3: Find the point representing 3 on your number line.
- Draw a closed circle (or a solid dot): The closed circle at 3 indicates that 3 is included in the solution set. This is because the inequality includes the "equal to" aspect.
- Shade to the left: Shade the number line to the left of 3. This represents all numbers less than 3.
[Visual representation of x ≤ 3 on a number line would be included here. Unfortunately, I cannot create images directly. Imagine a number line with a closed circle at 3 and the region to the left shaded.]
Inequalities with Negative Numbers
The same principles apply when dealing with negative numbers. For example, x ≤ -2:
- Locate -2: Find -2 on your number line.
- Closed circle: Draw a closed circle at -2.
- Shade to the left: Shade the number line to the left of -2, representing all numbers less than or equal to -2.
[Visual representation of x ≤ -2 on a number line would be included here. Again, imagine a number line with a closed circle at -2 and the region to the left shaded.]
Compound Inequalities
Compound inequalities combine multiple inequalities. For example, -1 ≤ x ≤ 5 means x is greater than or equal to -1 and less than or equal to 5. On the number line:
- Locate -1 and 5: Find -1 and 5 on the number line.
- Closed circles: Draw closed circles at both -1 and 5.
- Shade the region between: Shade the region between -1 and 5, inclusive. This represents all numbers between -1 and 5, including -1 and 5 themselves.
[Visual representation of -1 ≤ x ≤ 5 on a number line would be included here. Imagine a number line with closed circles at -1 and 5, with the region between them shaded.]
Practical Applications of ≤
The "less than or equal to" sign has widespread applications in various mathematical and real-world contexts:
1. Everyday Situations:
- Weight limits: A sign stating "Maximum weight ≤ 1000 kg" means the maximum permissible weight is 1000 kg or less.
- Speed limits: A speed limit sign indicating "Speed ≤ 60 mph" means the speed should be 60 mph or less.
- Age restrictions: An amusement park ride with a height restriction of "Height ≤ 48 inches" means only those whose height is 48 inches or less are allowed.
2. Algebra and Equations:
Solving inequalities involving "less than or equal to" is a fundamental aspect of algebra. The same rules of manipulating equations apply, with one key exception: multiplying or dividing by a negative number reverses the inequality sign.
Example: Solve for x: 2x + 3 ≤ 7
- Subtract 3 from both sides:
2x ≤ 4 - Divide both sides by 2:
x ≤ 2
This solution indicates that any value of x less than or equal to 2 satisfies the original inequality. On a number line, this would be represented by a closed circle at 2 and shading to the left.
3. Calculus and Advanced Mathematics:
The concept of "less than or equal to" is essential in calculus for defining intervals, limits, and determining the behavior of functions. For example, understanding inequalities is crucial when evaluating definite integrals or determining the convergence or divergence of infinite series.
4. Computer Science:
In computer programming and algorithm design, the "less than or equal to" operator is frequently used for conditional statements and loop control. For example, the code snippet:
for i in range(1, 11): # Range includes 1 and up to (but not including) 11
if i <= 5:
print(i)
This code will print the numbers 1 through 5 because the condition i <= 5 is true for those values.
5. Statistics and Data Analysis
Inequalities involving ≤ are essential for statistical analysis when defining confidence intervals, testing hypotheses or when dealing with cumulative distribution functions. For example, finding the probability that a random variable is less than or equal to a certain value relies heavily on understanding and manipulating inequalities.
Distinguishing ≤ from <
It's crucial to differentiate between "less than or equal to" (≤) and "less than" (<). The key difference lies in the inclusion of the equality aspect.
-
Less than (<):
a < bmeans 'a' is strictly less than 'b'. 'a' cannot be equal to 'b'. On a number line, this is represented by an open circle at 'b' and shading to the left. -
Less than or equal to (≤):
a ≤ bmeans 'a' is less than or equal to 'b'. 'a' can be less than 'b' or equal to 'b'. On a number line, this is represented by a closed circle at 'b' and shading to the left.
Failing to distinguish between these symbols can lead to incorrect solutions and misinterpretations of mathematical problems and real-world situations.
Solving More Complex Inequalities
Let's tackle a more complex inequality involving multiple variables and operations:
Solve for x: 3(x - 2) ≤ 5x + 4
- Distribute:
3x - 6 ≤ 5x + 4 - Subtract 3x from both sides:
-6 ≤ 2x + 4 - Subtract 4 from both sides:
-10 ≤ 2x - Divide both sides by 2:
-5 ≤ xThis is equivalent tox ≥ -5
This means x can be any number greater than or equal to -5. On a number line, this would be represented by a closed circle at -5 and shading to the right.
Conclusion
The "less than or equal to" sign (≤) is a fundamental mathematical symbol with broad applications across various fields. Understanding its meaning, its graphical representation on a number line, and its use in solving inequalities is essential for success in mathematics, computer science, and many other disciplines. This comprehensive guide provided a thorough overview, equipping you with the knowledge to confidently tackle inequalities and interpret their visual representations. Remember to carefully distinguish between ≤ and < to avoid errors in your calculations and interpretations. Consistent practice with various types of inequalities will further solidify your understanding and problem-solving skills.
Latest Posts
Latest Posts
-
Cuanto Es 16 Grados Fahrenheit En Centigrados
May 08, 2025
-
Which Of The Following Is An Algebraic Expression
May 08, 2025
-
How Much Is 6000 Lb In American Money
May 08, 2025
-
A Line Segment May Have More Than One Midpoint
May 08, 2025
-
Write 84 As A Product Of Prime Factors
May 08, 2025
Related Post
Thank you for visiting our website which covers about Less Than Or Equal To Sign On Number Line . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.