List Of All Perfect Square Roots
News Co
Apr 06, 2025 · 5 min read
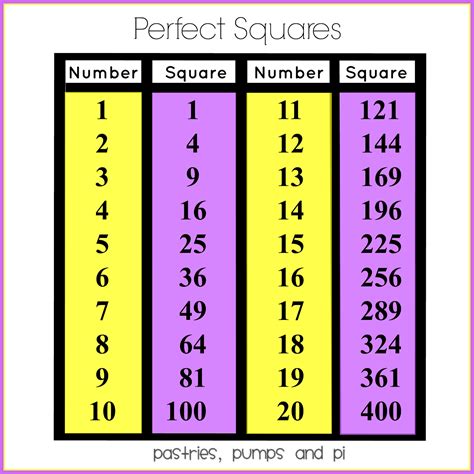
Table of Contents
The Enchanting World of Perfect Squares and Their Roots: A Comprehensive Guide
Perfect squares, those numbers that result from squaring an integer, hold a special place in mathematics. Understanding them is fundamental to various mathematical concepts, from basic algebra to advanced calculus. This comprehensive guide delves into the fascinating world of perfect squares, providing a detailed exploration of their properties, patterns, and applications. We’ll also tackle the seemingly simple yet endlessly intriguing question: what is a list of all perfect square roots?
While we can't provide an exhaustive list of all perfect square roots (as the sequence is infinite), we can explore the underlying principles, patterns, and methods to identify and understand them.
What is a Perfect Square?
A perfect square is a number that can be obtained by squaring an integer. In simpler terms, it's the result of multiplying an integer by itself. For example:
- 1 (1 x 1)
- 4 (2 x 2)
- 9 (3 x 3)
- 16 (4 x 4)
- 25 (5 x 5)
- and so on...
The integers used in this multiplication are called the square roots. Therefore, the square root of 9 is 3, because 3 x 3 = 9.
Understanding Square Roots
The square root of a number is a value that, when multiplied by itself, gives the original number. We denote the square root using the radical symbol (√). For instance:
- √9 = 3 (because 3 x 3 = 9)
- √16 = 4 (because 4 x 4 = 16)
- √25 = 5 (because 5 x 5 = 25)
It's crucial to understand that every positive number has two square roots: a positive and a negative one. For example, the square roots of 25 are +5 and -5 because both 5 x 5 = 25 and -5 x -5 = 25. However, when we talk about the square root, we usually refer to the positive square root.
Identifying Perfect Squares: Techniques and Tricks
While there's no definitive "list" of all perfect squares (as the sequence is infinite), understanding the underlying patterns can help you identify them quickly.
-
Recognizing Small Perfect Squares: Memorizing the perfect squares of the first few integers (1 to 20, for example) is a valuable skill. This allows for rapid identification of small perfect squares in calculations.
-
The Pattern of Differences: Observe the differences between consecutive perfect squares:
- 1 – 0 = 1
- 4 – 1 = 3
- 9 – 4 = 5
- 16 – 9 = 7
- 25 – 16 = 9
- ...and so on. The differences form an arithmetic sequence of odd numbers.
-
Using Prime Factorization: Prime factorization can help determine if a number is a perfect square. If every prime factor in the factorization has an even exponent, then the number is a perfect square. For example:
- 36 = 2² x 3² (both exponents are even, so 36 is a perfect square)
- 49 = 7² (exponent is even, so 49 is a perfect square)
- 50 = 2 x 5² (exponent of 2 is odd, so 50 is not a perfect square)
-
Calculating Larger Perfect Squares: For larger numbers, a calculator or computational tool is highly recommended to determine if a number is a perfect square. Modern calculators have built-in square root functions.
Applications of Perfect Squares
Perfect squares and their roots are fundamental to numerous mathematical concepts and applications across various fields:
-
Geometry: Calculating areas of squares, finding the lengths of sides in right-angled triangles (Pythagorean theorem), and solving geometric problems.
-
Algebra: Solving quadratic equations, simplifying algebraic expressions, and working with square roots in equations.
-
Calculus: Involving derivatives and integrals, the concept of perfect squares frequently surfaces in calculations.
-
Number Theory: Perfect squares play a vital role in number theory studies, relating to concepts like congruences and Diophantine equations.
-
Physics: Many physical phenomena and calculations rely on the concept of squares and square roots, like determining the energy of a particle or calculating velocities.
-
Computer Science: Algorithms and data structures frequently use the concept of squares and square roots in various applications.
Exploring the Infinite Sequence: Practical Considerations
While we can't list all perfect squares, we can generate them indefinitely. The sequence of perfect squares is:
1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256, 289, 324, 361, 400… and so on to infinity.
This sequence is generated by squaring successive integers (n² where n is an integer).
Dealing with Non-Perfect Squares and Approximations
Not all numbers are perfect squares. When dealing with non-perfect squares, we often use approximations or decimal representations of their square roots. Calculators and software provide precise decimal approximations. For example, the square root of 2 (√2) is approximately 1.414.
Beyond the Basics: Advanced Concepts Related to Perfect Squares
The world of perfect squares extends beyond the basics. Advanced concepts include:
-
Sums of Squares: Exploring the conditions under which sums of squares result in other perfect squares.
-
Difference of Squares: Understanding how the difference between two squares can be factored.
-
Perfect Square Trinomials: Recognizing and factoring algebraic expressions that are perfect square trinomials.
Conclusion: Embracing the Beauty of Perfect Squares
Understanding perfect squares and their square roots is essential for anyone pursuing a path in mathematics or related fields. While a complete list is impossible due to the infinite nature of the sequence, understanding the principles, patterns, and techniques presented here will empower you to identify, manipulate, and apply perfect squares effectively in various mathematical contexts. The elegance and simplicity of perfect squares belies their deep significance and far-reaching applications, making them a captivating subject for both novice and expert mathematicians alike. The journey of exploring perfect squares is a continuous one, full of interesting patterns and unexpected connections. By embracing the beauty of these fundamental mathematical concepts, one can unlock deeper mathematical understanding and appreciation for the fascinating world of numbers.
Latest Posts
Related Post
Thank you for visiting our website which covers about List Of All Perfect Square Roots . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.