Next Number 2 7 8 3 12 9
News Co
Apr 10, 2025 · 5 min read
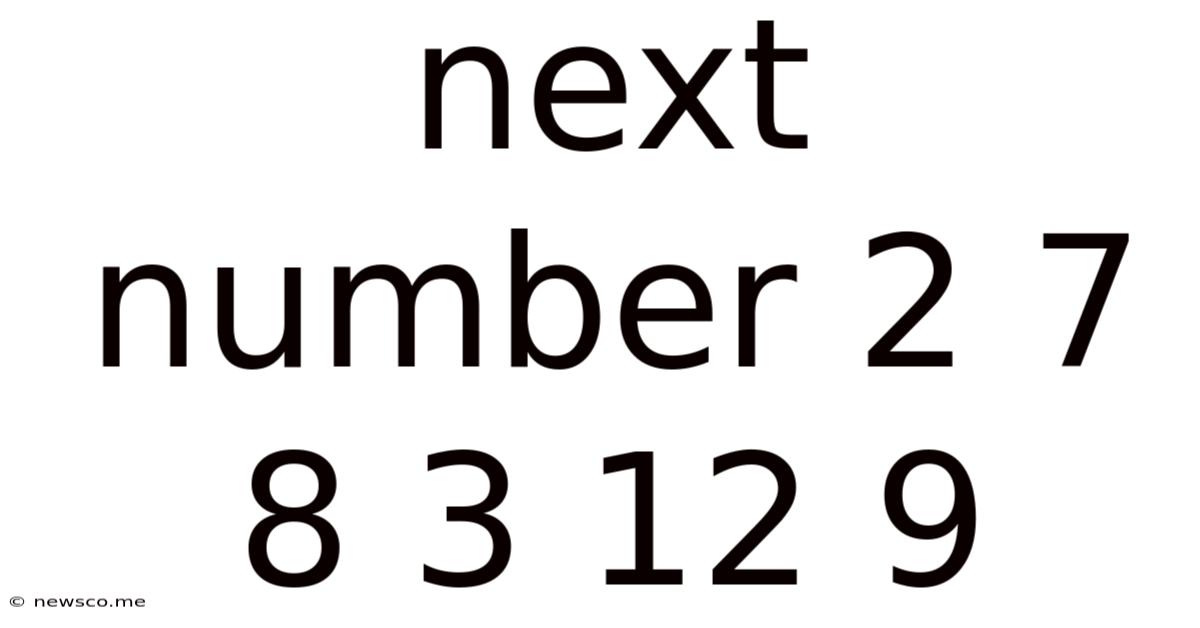
Table of Contents
Decoding the Sequence: Unraveling the Mystery of 2, 7, 8, 3, 12, 9
The seemingly simple sequence 2, 7, 8, 3, 12, 9 presents a fascinating challenge for those who enjoy number puzzles and mathematical pattern recognition. At first glance, it appears chaotic, lacking any immediately obvious arithmetic progression. However, a deeper dive reveals that this sequence isn't random; it harbors a hidden logic waiting to be uncovered. This article will explore various approaches to deciphering this sequence, highlighting different mathematical concepts and problem-solving strategies. We'll investigate potential patterns, explore alternative interpretations, and ultimately strive to determine the next number in the sequence.
Potential Approaches to Deciphering the Sequence
Several methods can be applied to analyze this intriguing numerical puzzle. Let's explore some of the most promising avenues:
1. Analyzing Differences and Patterns:
A common approach to deciphering number sequences involves examining the differences between consecutive numbers. Let's analyze the differences in our sequence:
- 7 - 2 = 5
- 8 - 7 = 1
- 3 - 8 = -5
- 12 - 3 = 9
- 9 - 12 = -3
The differences (5, 1, -5, 9, -3) don't immediately reveal a simple pattern. However, let's look at the differences of the differences:
- 1 - 5 = -4
- -5 - 1 = -6
- 9 - (-5) = 14
- -3 - 9 = -12
Again, no clear pattern emerges. This suggests that a simpler arithmetic progression might not be the solution.
2. Exploring Alternative Mathematical Relationships:
Perhaps the relationship between numbers isn't purely additive or subtractive. Let's consider other possibilities:
- Prime Numbers and Composites: Notice that some numbers are prime (2, 3, 7) while others are composite (8, 9, 12). This could be a clue, but it doesn't immediately lead to a straightforward pattern.
- Modular Arithmetic: Examining the remainders when dividing by a specific number might reveal a pattern. For example, considering remainders when divided by 3: (2, 1, 2, 0, 0, 0). This is intriguing but doesn't instantly offer a conclusive prediction for the next number.
- Geometric Progressions: There's no apparent geometric progression in this sequence (multiplying by a constant factor to get the next number).
- Fibonacci-like Sequences: While not a strict Fibonacci sequence (where each number is the sum of the two preceding numbers), let's explore if there's a variation. The differences aren't directly related in a Fibonacci fashion.
3. Considering External Factors:
Sometimes, the solution lies outside purely mathematical relationships. Could there be other hidden codes or patterns?
- Alphabetical Representation: Assigning numerical values to letters (A=1, B=2, etc.) and exploring word associations or anagrams isn't likely productive in this case, as there's no apparent link to language.
- Hidden Formulas: It's possible that a more complex formula generates the sequence, possibly involving multiple operations and variables. This requires a more advanced mathematical approach, perhaps involving polynomial equations or other advanced mathematical functions.
Advanced Mathematical Approaches and Potential Solutions
Let's delve into more complex methods for analyzing the sequence.
1. Polynomial Interpolation:
Polynomial interpolation is a technique used to find a polynomial that passes through a set of given points. We can use this to fit a curve to our data points (the sequence numbers). However, even with sophisticated software, finding a polynomial that perfectly fits this sequence could yield an excessively complex equation, lacking elegance or predictability. Furthermore, finding the next number would depend entirely on the chosen polynomial, which could lead to multiple potential solutions.
2. Recursive Relationships:
A recursive relationship defines each term in the sequence as a function of preceding terms. While no obvious recursive relationship jumps out, it's possible that a more complex recursive formula exists. This would require extensive trial and error or the use of specialized mathematical software to discover a fitting recursive definition.
3. Exploring Hidden Patterns through Data Visualization:
Graphing the sequence might reveal hidden patterns not immediately apparent in the raw numerical data. Plotting the numbers against their indices (position in the sequence) might show a trend or suggest a functional relationship that can be modeled mathematically. However, with only six data points, it is difficult to conclusively determine a definitive pattern through visualization alone.
The Limitations of Finding a Definitive Answer
It's important to acknowledge the inherent limitations in determining a single definitive next number in this sequence. Without additional context or a stated generation rule, multiple plausible solutions can exist, each supported by a different mathematical interpretation.
Illustrative Examples of Potential Next Numbers and Their Justifications (Hypothetical)
It's crucial to understand that any proposed next number is a hypothesis, based on a specific interpretation of potential underlying patterns. There is no single "correct" answer without further information.
For example:
-
Hypothesis 1 (Based on a loose pattern in differences): We could attempt to find a loose pattern in the differences between the differences from our earlier analysis, potentially leading to a next difference of -18. Adding this to 9 (the last number) gives us a potential next number of -9. This is highly speculative and lacks strong mathematical justification.
-
Hypothesis 2 (Based on a hypothetical recursive relationship): A complex recursively defined function could be contrived to fit the sequence, producing any chosen next number. This method, however, lacks predictive power and lacks generalizability.
-
Hypothesis 3 (Acknowledging the lack of a discernible pattern): We could conclude that the sequence has no readily apparent pattern and the next number could be essentially any number, chosen arbitrarily.
Conclusion: Embracing the Ambiguity
The sequence 2, 7, 8, 3, 12, 9 remains a fascinating puzzle. While we explored several analytical approaches, including differences analysis, alternative mathematical relationships, and advanced methods like polynomial interpolation and recursive relationships, a single, definitively correct next number remains elusive. The exercise highlights the importance of considering various problem-solving strategies and the inherent limitations in predicting patterns from limited data. The very ambiguity of this puzzle serves as a valuable learning experience, showcasing the rich and diverse landscape of mathematical reasoning and the creativity involved in pattern recognition. It encourages critical thinking and the exploration of different mathematical possibilities. The true solution might only be revealed if additional information is provided about the origin or generating rule of this numerical sequence.
Latest Posts
Related Post
Thank you for visiting our website which covers about Next Number 2 7 8 3 12 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.