Numbers With An Odd Number Of Factors
News Co
Apr 18, 2025 · 6 min read
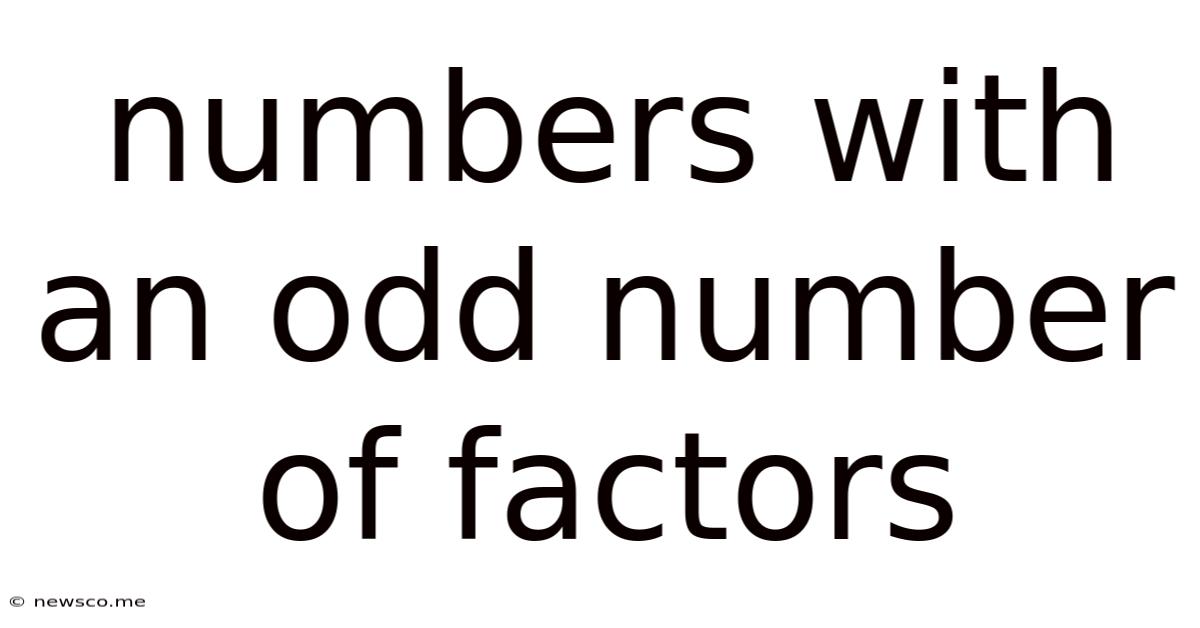
Table of Contents
Numbers with an Odd Number of Factors: A Deep Dive into Number Theory
The world of mathematics is brimming with fascinating patterns and intriguing properties. One such area of exploration delves into the realm of numbers and their factors, specifically, those numbers possessing an odd number of factors. This seemingly simple concept opens a gateway to a deeper understanding of prime factorization, perfect squares, and the elegance inherent in number theory. This article will explore the characteristics of these unique numbers, providing clear explanations and examples to illuminate this fascinating mathematical concept.
Understanding Factors and Factorization
Before we dive into the specifics of numbers with an odd number of factors, let's establish a firm grasp on the fundamental concepts. A factor (or divisor) of a number is a whole number that divides the number evenly, leaving no remainder. For instance, the factors of 12 are 1, 2, 3, 4, 6, and 12.
Prime factorization is the process of expressing a number as a product of its prime factors. A prime number is a whole number greater than 1 that has only two factors: 1 and itself. For example, the prime factorization of 12 is 2² x 3. This means 12 can be expressed as 2 x 2 x 3.
Understanding prime factorization is crucial because it provides the key to determining the number of factors a given number possesses.
The Number of Factors: A Formulaic Approach
The number of factors a number has can be calculated using its prime factorization. Let's say a number 'n' has the prime factorization:
n = p₁<sup>a₁</sup> * p₂<sup>a₂</sup> * p₃<sup>a₃</sup> ... * p<sub>k</sub><sup>a<sub>k</sub></sup>
where p₁, p₂, ..., p<sub>k</sub> are distinct prime numbers and a₁, a₂, ..., a<sub>k</sub> are their respective exponents.
The total number of factors of 'n' is given by the formula:
(a₁ + 1)(a₂ + 1)(a₃ + 1)...(a<sub>k</sub> + 1)
For example, let's find the number of factors of 12 (2² x 3¹):
Number of factors = (2 + 1)(1 + 1) = 3 x 2 = 6
This confirms our earlier observation that 12 has six factors (1, 2, 3, 4, 6, 12).
The Odd Number of Factors Enigma
Now, let's address the central theme: numbers with an odd number of factors. Observe that the formula for the number of factors involves a product of terms (aᵢ + 1). For the product to be odd, each of the terms (aᵢ + 1) must be odd. This implies that each exponent (aᵢ) must be an even number.
If all the exponents in the prime factorization are even, it means that each prime factor is raised to an even power. This leads us to a crucial conclusion: a number has an odd number of factors if and only if it is a perfect square.
Perfect Squares: The Key to Odd Factor Counts
A perfect square is a number that can be obtained by squaring an integer. For example, 9 (3²) and 16 (4²) are perfect squares. The prime factorization of a perfect square always involves even exponents for each prime factor.
Let's illustrate this with an example: consider the number 36. Its prime factorization is 2² x 3². Using the formula for the number of factors:
Number of factors = (2 + 1)(2 + 1) = 9
The factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, and 36 – nine factors in total, an odd number.
Conversely, a number that is not a perfect square will always have an even number of factors. This is because at least one of the exponents in its prime factorization will be odd, resulting in an even product in the factor count formula.
Deeper Exploration: Properties and Applications
The concept of numbers with an odd number of factors extends beyond a simple mathematical curiosity. It has implications in various areas of mathematics and even finds practical applications.
1. Connecting to Other Mathematical Concepts
The relationship between perfect squares and the odd number of factors provides a bridge to connect various mathematical concepts. It helps illustrate the power of prime factorization and its role in understanding the properties of numbers. It also reinforces the importance of understanding fundamental concepts like prime numbers and exponents.
2. Applications in Advanced Number Theory
In advanced number theory, the study of numbers with an odd number of factors contributes to a deeper understanding of number structures and patterns. This knowledge can be applied to various areas of mathematics, such as cryptography and coding theory. The concept of perfect squares and their factor properties plays a significant role in analyzing the distribution of numbers and their relationships.
3. Problem Solving and Mathematical Puzzles
The concept frequently appears in mathematical puzzles and problem-solving exercises. Understanding the relationship between perfect squares and the number of factors allows for efficient problem-solving techniques. For instance, if a problem involves finding a number with an odd number of factors, you can immediately focus on perfect squares.
Examples and Exercises
Let's solidify our understanding with some examples and exercises:
Example 1: Does the number 100 have an odd number of factors?
The prime factorization of 100 is 2² x 5². Since the exponents are both even, 100 is a perfect square, and it has an odd number of factors. Indeed, 100 has (2+1)(2+1) = 9 factors.
Example 2: Find a number between 50 and 100 that has an odd number of factors.
We need to find a perfect square in this range. The perfect squares are 64 (8²) and 81 (9²). Both 64 and 81 have an odd number of factors.
Exercise 1: Determine the number of factors for each of the following numbers and state whether the number of factors is odd or even:
- 144
- 169
- 200
- 225
- 289
Exercise 2: Find three numbers between 100 and 200 that have an odd number of factors. Explain your reasoning.
Exercise 3: Prove that if a number has exactly three factors, it must be the square of a prime number.
By working through these examples and exercises, you will further develop your understanding of numbers with an odd number of factors and their connection to perfect squares.
Conclusion: The Beauty of Mathematical Patterns
The exploration of numbers with an odd number of factors reveals the elegance and underlying order within the seemingly chaotic world of numbers. This simple yet profound concept serves as a testament to the power of mathematical reasoning and the interconnectedness of mathematical ideas. By understanding the principles of prime factorization and perfect squares, we can unlock a deeper appreciation for the fascinating patterns and structures that govern the numerical world. The knowledge gained provides valuable tools for problem-solving and further exploration into the rich tapestry of number theory.
Latest Posts
Related Post
Thank you for visiting our website which covers about Numbers With An Odd Number Of Factors . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.