Opposite Angles Of A Parallelogram Are Equal
News Co
Apr 17, 2025 · 5 min read
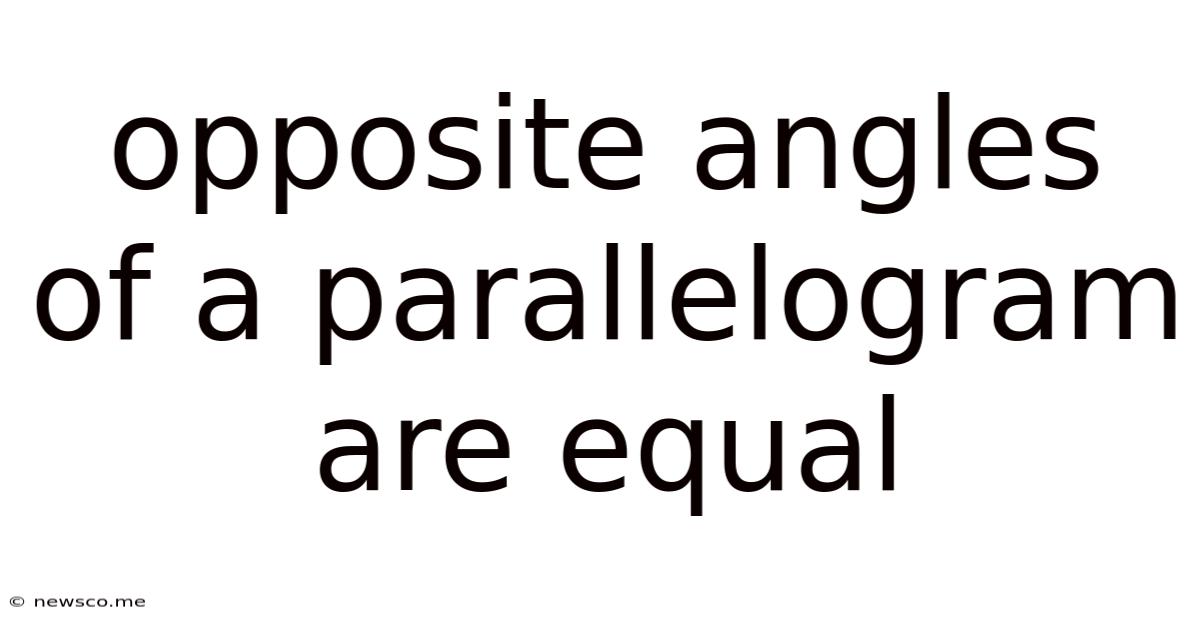
Table of Contents
Opposite Angles of a Parallelogram are Equal: A Comprehensive Guide
Understanding the properties of geometric shapes is fundamental to various fields, from architecture and engineering to computer graphics and game development. One such crucial property lies within parallelograms: their opposite angles are always equal. This seemingly simple fact forms the basis of many geometric proofs and applications. This article delves deep into this property, exploring its proof, implications, and applications in diverse contexts. We'll break down the concept in an accessible way, suitable for students, enthusiasts, and professionals alike.
Understanding Parallelograms
Before diving into the proof, let's establish a clear understanding of what a parallelogram is. A parallelogram is a quadrilateral (a four-sided polygon) with opposite sides parallel. This seemingly simple definition gives rise to a series of interesting properties, including the equality of opposite angles, which is the focus of this article.
Other key characteristics of parallelograms include:
- Opposite sides are equal in length: This means that the lengths of opposite sides are congruent.
- Opposite angles are equal in measure: This is the core concept we'll be exploring in detail.
- Consecutive angles are supplementary: This means that the sum of any two consecutive angles (angles that share a side) is 180 degrees.
- Diagonals bisect each other: The diagonals of a parallelogram intersect at their midpoints.
Proving that Opposite Angles of a Parallelogram are Equal
Several methods can be used to prove that opposite angles of a parallelogram are equal. We'll explore a common and intuitive approach using parallel lines and transversal properties.
Method 1: Using Parallel Lines and Transversals
Consider a parallelogram ABCD, where AB is parallel to CD and BC is parallel to AD. Let's focus on angles A and C.
-
Parallel Lines and a Transversal: Line BC acts as a transversal intersecting the parallel lines AB and CD. This creates several pairs of angles with specific relationships.
-
Alternate Interior Angles: Angles ABC and BCD are alternate interior angles. A fundamental property of parallel lines states that alternate interior angles are equal. Therefore, ∠ABC = ∠BCD.
-
Parallel Lines and Another Transversal: Similarly, line AD acts as a transversal intersecting the parallel lines AB and CD. This creates another pair of alternate interior angles: ∠BAD and ∠ADC. Therefore, ∠BAD = ∠ADC.
-
Conclusion: We've shown that ∠ABC = ∠BCD and ∠BAD = ∠ADC. This proves that opposite angles in a parallelogram are equal. This logic holds true for any parallelogram, regardless of its dimensions or shape.
Applications and Implications
The property of equal opposite angles in parallelograms has numerous applications across various fields:
1. Geometry and Geometric Proofs
This property is crucial for solving geometric problems and constructing more complex proofs. Many theorems and postulates rely on this fundamental characteristic of parallelograms. For instance, proving that a quadrilateral is a parallelogram often involves demonstrating the equality of opposite angles.
2. Architecture and Engineering
In architecture and engineering, understanding parallelogram properties is vital for structural design and stability analysis. Many structures utilize parallelogram-shaped components, and the predictability of their angles ensures structural integrity. For instance, the supporting framework of a roof might incorporate parallelogram shapes, relying on the angle consistency for load distribution.
3. Computer Graphics and Game Development
In computer graphics and game development, the properties of parallelograms are used extensively in transformations and rendering. Representing objects using parallelograms allows for efficient calculations and animations. Game engines often utilize parallelogram-based collision detection systems, leveraging the predictable angles for accurate object interaction.
4. Physics and Mechanics
In physics and mechanics, the understanding of parallelograms finds application in force and vector analysis. Representing forces as vectors and utilizing parallelogram laws for vector addition and resolution is commonplace.
Special Cases of Parallelograms
Parallelograms have several special cases, each with unique properties that build upon the fundamental concept of equal opposite angles:
1. Rectangles
A rectangle is a parallelogram where all four angles are right angles (90 degrees). Since opposite angles are equal in any parallelogram, in a rectangle, all four angles are equal to 90 degrees.
2. Rhombuses
A rhombus is a parallelogram where all four sides are equal in length. While opposite angles remain equal, the angles themselves are not necessarily 90 degrees.
3. Squares
A square is a special case of both a rectangle and a rhombus. It's a parallelogram with four equal sides and four right angles. Therefore, it possesses all the properties of parallelograms, rectangles, and rhombuses, including equal opposite angles.
Advanced Applications and Further Exploration
The principle of equal opposite angles in parallelograms extends to more advanced mathematical concepts:
- Linear Algebra: In linear algebra, the concepts of vectors and matrices frequently utilize parallelograms for representing transformations and operations.
- Higher-Dimensional Geometry: The concept of equal opposite angles extends to higher-dimensional parallelepipeds and other geometric structures.
- Topology: The properties of parallelograms, including the equality of opposite angles, play a role in topological studies of surfaces and shapes.
Conclusion
The seemingly simple property that opposite angles of a parallelogram are equal is a cornerstone of geometry and has significant implications across various disciplines. Its proof, rooted in the fundamental principles of parallel lines and transversals, provides a solid foundation for understanding this property. From architecture and engineering to computer graphics and game development, the application of this principle is far-reaching, demonstrating the practical utility of even seemingly basic geometric concepts. By understanding this property, we unlock a deeper appreciation for the elegance and power of geometrical principles in shaping the world around us. Continued exploration of this and related properties will undoubtedly lead to further innovations and discoveries in numerous fields.
Latest Posts
Related Post
Thank you for visiting our website which covers about Opposite Angles Of A Parallelogram Are Equal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.