P 2w 2l Solve For W
News Co
Apr 26, 2025 · 5 min read
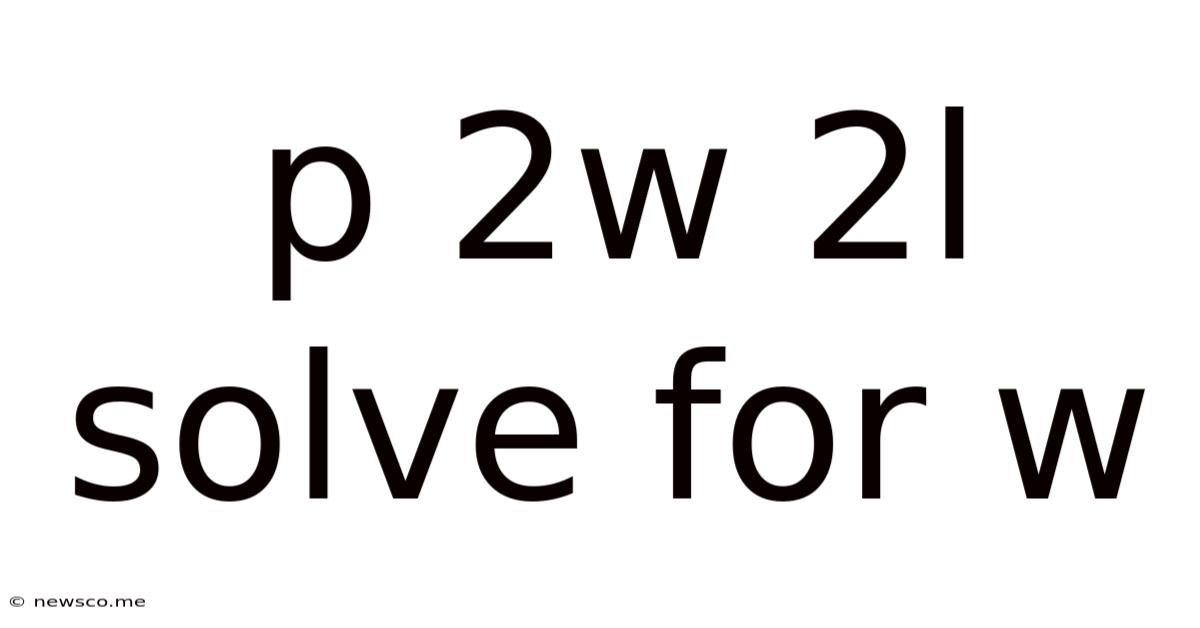
Table of Contents
Solving for 'w': A Comprehensive Guide to P = 2w + 2l
This article provides a detailed explanation of how to solve for the variable 'w' in the equation P = 2w + 2l, commonly used in calculating the perimeter of a rectangle. We'll cover various approaches, delve into the underlying mathematical principles, and provide practical examples to solidify your understanding. This guide is designed for students of all levels, from those just beginning their algebra journey to those seeking a refresher on fundamental algebraic manipulation. We'll also touch on the applications of this formula beyond basic geometry.
Understanding the Equation: P = 2w + 2l
Before we jump into solving for 'w', let's break down the equation itself. This equation represents the perimeter (P) of a rectangle, where:
- P represents the perimeter of the rectangle (the total distance around the outside).
- w represents the width of the rectangle.
- l represents the length of the rectangle.
The equation states that the perimeter is equal to twice the width plus twice the length. This makes intuitive sense: you have two widths and two lengths that make up the rectangle's perimeter.
Solving for 'w': Step-by-Step Guide
Our goal is to isolate 'w' on one side of the equation. This involves applying algebraic principles to rearrange the terms. Here's a step-by-step guide:
Step 1: Subtract 2l from both sides
To begin isolating 'w', we need to remove the '2l' term from the right-hand side of the equation. We can do this by subtracting '2l' from both sides of the equation. This maintains the equality:
P - 2l = 2w + 2l - 2l
This simplifies to:
P - 2l = 2w
Step 2: Divide both sides by 2
Now, we have '2w' on the right-hand side. To isolate 'w', we need to divide both sides of the equation by 2:
(P - 2l) / 2 = 2w / 2
This simplifies to:
w = (P - 2l) / 2
Therefore, the solution for 'w' is:
w = (P - 2l) / 2
This equation now allows you to calculate the width ('w') of a rectangle if you know its perimeter ('P') and length ('l').
Practical Applications and Examples
Let's work through a few examples to illustrate the application of this formula:
Example 1:
A rectangular garden has a perimeter of 20 meters and a length of 6 meters. What is the width of the garden?
- Identify the knowns: P = 20 meters, l = 6 meters.
- Substitute the values into the formula: w = (20 - (2 * 6)) / 2
- Solve the equation: w = (20 - 12) / 2 = 8 / 2 = 4 meters.
Therefore, the width of the garden is 4 meters.
Example 2:
A rectangular swimming pool has a perimeter of 36 feet and a width of 7 feet. What is the length of the pool?
This example demonstrates how, once you've solved for 'w', you can rearrange the formula to solve for 'l':
- Start with the solved equation: w = (P - 2l) / 2
- Rearrange to solve for 'l': Multiply both sides by 2: 2w = P - 2l. Add 2l to both sides: 2w + 2l = P. Subtract 2w from both sides: 2l = P - 2w. Divide both sides by 2: l = (P - 2w) / 2
- Substitute the values: l = (36 - (2 * 7)) / 2
- Solve the equation: l = (36 - 14) / 2 = 22 / 2 = 11 feet.
Therefore, the length of the swimming pool is 11 feet.
Beyond Rectangles: Applications in Other Fields
While the formula P = 2w + 2l is fundamentally linked to rectangular geometry, the principles of solving for variables within an equation have much broader applications. Understanding how to manipulate algebraic expressions is crucial in various fields, including:
-
Physics: Many physics equations involve multiple variables, and solving for a specific variable is often necessary to determine an unknown quantity. For example, equations related to motion, forces, and energy frequently require this type of algebraic manipulation.
-
Engineering: Engineers regularly use algebraic equations to model and analyze systems. Solving for specific variables is essential for determining design parameters, predicting system performance, and troubleshooting problems.
-
Finance: Financial calculations often involve equations with multiple variables, such as interest rates, principal amounts, and time periods. Solving for specific variables allows for the determination of unknown financial quantities.
-
Computer Science: In programming and algorithm design, algebraic manipulation is frequently needed to optimize code, solve for specific data values, and develop efficient algorithms.
Advanced Concepts and Further Exploration
For those seeking a deeper understanding, several advanced concepts build upon the foundation of solving for 'w' in P = 2w + 2l:
-
Simultaneous Equations: If you have two or more equations involving the same variables, you can use techniques like substitution or elimination to solve for all the unknowns simultaneously.
-
Quadratic Equations: More complex geometric problems may involve quadratic equations (equations with squared terms). Solving quadratic equations requires different techniques, such as factoring, the quadratic formula, or completing the square.
-
Calculus: Calculus provides tools for analyzing rates of change and optimizing functions, which are often expressed using algebraic equations.
Conclusion: Mastering the Fundamentals
The ability to solve for 'w' in the equation P = 2w + 2l, and more generally, to manipulate algebraic equations, is a fundamental skill with broad applications across various disciplines. By understanding the underlying principles and practicing with examples, you'll build a strong foundation for tackling more complex mathematical problems in the future. Remember, the key is to systematically apply algebraic rules to isolate the desired variable, always maintaining the equality of the equation throughout the process. Continue practicing, explore advanced concepts, and you'll soon master this essential skill.
Latest Posts
Related Post
Thank you for visiting our website which covers about P 2w 2l Solve For W . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.