Perimeter Of Right Angle Triangle Formula
News Co
Apr 05, 2025 · 5 min read
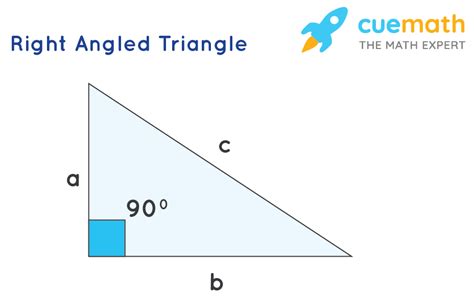
Table of Contents
Understanding and Applying the Perimeter of a Right-Angled Triangle Formula
The perimeter of any polygon, including a right-angled triangle, is simply the total distance around its outside. For a right-angled triangle, this means adding the lengths of all three sides: the two shorter sides (legs or cathetus) and the longest side (hypotenuse). While seemingly straightforward, understanding the nuances of calculating the perimeter, especially when dealing with unknown side lengths, requires a grasp of fundamental geometric principles and, sometimes, the application of the Pythagorean theorem. This comprehensive guide will delve into the formula, its applications, and various scenarios you might encounter.
The Basic Formula: A Simple Start
The perimeter (P) of a right-angled triangle is given by the formula:
P = a + b + c
Where:
- a and b represent the lengths of the two shorter sides (legs) of the right-angled triangle.
- c represents the length of the hypotenuse (the side opposite the right angle).
This formula is universally applicable, regardless of the triangle's size or orientation. The key is accurately measuring or determining the lengths of all three sides.
Calculating the Perimeter: Step-by-Step Examples
Let's illustrate the perimeter calculation with some examples, starting with a simple case where all side lengths are known:
Example 1: All Sides Given
Imagine a right-angled triangle with sides measuring a = 3 cm, b = 4 cm, and c = 5 cm. Applying the formula:
P = 3 cm + 4 cm + 5 cm = 12 cm
Therefore, the perimeter of this right-angled triangle is 12 cm.
Example 2: Using the Pythagorean Theorem
Often, you'll only know the lengths of two sides. In a right-angled triangle, if you know the lengths of the two shorter sides (a and b), you can calculate the hypotenuse (c) using the Pythagorean theorem:
a² + b² = c²
Let's say a = 6 cm and b = 8 cm. We can find c:
6² + 8² = c² 36 + 64 = c² 100 = c² c = √100 = 10 cm
Now that we have all three side lengths, we can calculate the perimeter:
P = 6 cm + 8 cm + 10 cm = 24 cm
The perimeter of this right-angled triangle is 24 cm.
Example 3: One Leg and Hypotenuse Given
Suppose you know the length of one leg (a) and the hypotenuse (c). You can use the Pythagorean theorem to find the other leg (b):
c² - a² = b²
Let's say a = 5 cm and c = 13 cm. Then:
13² - 5² = b² 169 - 25 = b² 144 = b² b = √144 = 12 cm
Now calculate the perimeter:
P = 5 cm + 12 cm + 13 cm = 30 cm
Advanced Applications and Problem-Solving
The perimeter formula for a right-angled triangle becomes more involved when dealing with complex scenarios involving angles, areas, or other geometric properties.
Using Trigonometric Functions
If you know one leg and an angle (other than the right angle), you can use trigonometric functions (sine, cosine, tangent) to find the other sides and then calculate the perimeter.
For instance, if you know leg 'a' and angle A (opposite to leg 'a'), you can use:
- tan(A) = a/b to find b.
- sin(A) = a/c to find c.
Once you've found b and c, you can compute the perimeter using the standard formula.
Relationship with Area
The area of a right-angled triangle is given by:
Area = (1/2) * a * b
Sometimes, you might be given the area and one leg, allowing you to calculate the other leg and subsequently the hypotenuse and perimeter.
Word Problems and Real-World Applications
Right-angled triangles are prevalent in various real-world applications, including:
- Construction: Calculating the length of diagonal supports, roof slopes, and other structural elements.
- Navigation: Determining distances and directions using triangulation methods.
- Surveying: Measuring land areas and plotting boundaries.
- Engineering: Designing ramps, bridges, and other structures.
Understanding how to calculate the perimeter is crucial for solving many practical problems within these fields. For example, a contractor might need to calculate the perimeter of a triangular section of a building's foundation to determine the amount of material needed.
Common Mistakes and How to Avoid Them
Several common mistakes can occur when calculating the perimeter of a right-angled triangle:
- Incorrect application of the Pythagorean theorem: Ensure you are using the correct formula (a² + b² = c²) and correctly solving for the unknown side.
- Unit inconsistencies: Maintain consistent units throughout your calculations (e.g., all measurements in centimeters or meters).
- Rounding errors: Avoid excessive rounding during intermediate calculations, which can lead to significant errors in the final answer. Round only at the very end.
- Confusing area and perimeter: Remember that the area and perimeter are distinct concepts. Don't accidentally use the area formula when calculating the perimeter.
Expanding Your Knowledge: Beyond the Basics
While this guide focuses on the fundamental aspects of calculating the perimeter of a right-angled triangle, numerous advanced concepts build upon this foundation. Exploring these can significantly enhance your understanding of geometry and problem-solving skills:
Similar Triangles
Understanding similar triangles allows you to apply proportional relationships to solve problems where only some side lengths are known. If two right-angled triangles are similar, the ratio of corresponding sides will be constant.
Isosceles Right-Angled Triangles
These triangles have two legs of equal length. This simplification can make calculations easier, as you only need to know one leg length to determine all side lengths.
Equilateral Triangles (Indirectly Related)
Although not directly right-angled triangles, understanding the properties of equilateral triangles (all sides equal) is helpful in related geometric problem-solving.
Advanced Geometric Theorems
Exploring theorems like the Law of Cosines and the Law of Sines extends the perimeter calculation to more general triangles and expands your ability to handle various geometric challenges.
Conclusion: Mastering Perimeter Calculations
Mastering the calculation of the perimeter of a right-angled triangle is a crucial stepping stone in understanding geometry and its real-world applications. By thoroughly grasping the fundamental formula, the Pythagorean theorem, and various problem-solving techniques, you equip yourself with a valuable skill set applicable across various disciplines. Remember to practice regularly, identify potential pitfalls, and continually expand your knowledge to handle increasingly complex geometric problems effectively. The ability to accurately and efficiently calculate perimeters directly contributes to accurate measurements and successful problem-solving in many fields.
Latest Posts
Related Post
Thank you for visiting our website which covers about Perimeter Of Right Angle Triangle Formula . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.