Point B Is The Midpoint Of Ac
News Co
Apr 27, 2025 · 5 min read
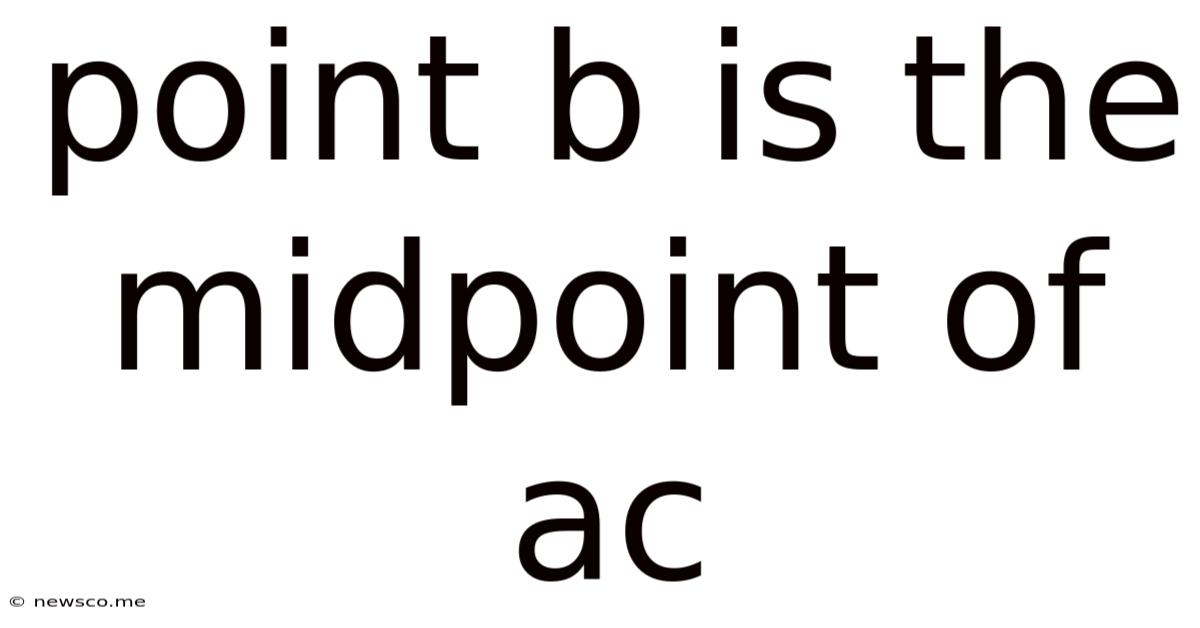
Table of Contents
Point B is the Midpoint of AC: A Comprehensive Exploration
Finding the midpoint of a line segment is a fundamental concept in geometry with far-reaching applications in various fields. This article delves deep into the concept of point B being the midpoint of line segment AC, exploring its implications, applications, and related mathematical concepts. We'll cover everything from the basic definition and formula to more advanced applications and problem-solving techniques. By the end, you'll have a solid understanding of midpoints and their significance in mathematics.
Understanding Midpoints: The Basics
A midpoint is a point that divides a line segment into two equal segments. In simpler terms, it's the exact middle point of a line. If point B is the midpoint of line segment AC, then the distance from A to B is equal to the distance from B to C. This can be represented symbolically as AB = BC.
Defining the Line Segment AC
Before we delve into the specifics of B being the midpoint, let's define the line segment AC itself. A line segment is a portion of a line that is bounded by two distinct endpoints, in this case, points A and C. It has a defined length, unlike a line that extends infinitely in both directions.
The Midpoint Formula: A Powerful Tool
The midpoint formula provides a straightforward way to calculate the coordinates of the midpoint of a line segment given the coordinates of its endpoints. If point A has coordinates (x₁, y₁) and point C has coordinates (x₂, y₂), then the coordinates of the midpoint B (xₘ, yₘ) are given by:
xₘ = (x₁ + x₂) / 2
yₘ = (y₁ + y₂) / 2
This formula is incredibly useful for solving various geometric problems, as we'll see in the following sections.
Applications of the Midpoint Theorem
The concept of a midpoint and the midpoint formula have widespread applications across diverse fields:
1. Geometry and Coordinate Geometry:
- Finding the center of a circle: If you know two endpoints of a diameter of a circle, the midpoint of that diameter is the center of the circle. This is a crucial concept in circle geometry.
- Constructing perpendicular bisectors: The midpoint of a line segment is essential for constructing the perpendicular bisector of that segment. This is a fundamental construction in geometry.
- Solving geometric proofs: The midpoint theorem plays a crucial role in many geometric proofs, simplifying complex relationships between points and lines. Understanding midpoint properties often allows for elegant and efficient solutions.
- Dividing line segments proportionally: The midpoint divides a line segment into a ratio of 1:1. Extending this concept, you can use the section formula to find points that divide a line segment into other ratios.
2. Computer Graphics and Computer-Aided Design (CAD):
- Image manipulation: Midpoints are critical in image processing and manipulation software. They are used in various transformations and algorithms, such as scaling, rotation, and translation.
- 3D modeling: Midpoints are crucial in 3D modeling and animation, enabling precise control over object placement, manipulation, and smooth transitions.
- Game development: Midpoints are fundamental in creating realistic movement and collision detection in video games.
3. Physics and Engineering:
- Calculating centroids: The centroid of a geometric shape is the average position of all points in the shape. The concept of midpoints aids in determining the centroids of various shapes, essential in structural analysis and mechanics.
- Determining center of mass: The center of mass is a crucial concept in physics, and often involves calculating midpoints to determine the equilibrium point of an object.
- Navigation and surveying: Midpoints are utilized in various surveying and navigation techniques to determine precise locations and distances.
4. Real-World Applications:
- Construction and architecture: Midpoints play a significant role in construction and architecture, ensuring precise measurements and accurate placement of structural elements.
- Cartography: In mapmaking, midpoints are used for determining distances and locations accurately.
- Graphic design: In graphic design, midpoints can be used to center objects or create symmetrical layouts.
Advanced Concepts and Problem Solving
Let's delve into some more advanced concepts related to midpoints and how to tackle complex problems:
1. The Midpoint Theorem and Triangles
The midpoint theorem states that the line segment connecting the midpoints of two sides of a triangle is parallel to the third side and is half its length. This theorem has extensive applications in geometric proofs and problem-solving.
2. Vectors and Midpoints
Midpoints can be elegantly represented using vectors. If a and c represent the position vectors of points A and C respectively, then the position vector b of the midpoint B is given by:
b = (a + c) / 2
This vector representation simplifies many calculations and proofs involving midpoints.
3. Solving Problems Involving Midpoints
Let's tackle a sample problem to illustrate the application of these concepts:
Problem: Point A has coordinates (2, 4) and point C has coordinates (8, 10). Find the coordinates of the midpoint B.
Solution: Using the midpoint formula:
- xₘ = (2 + 8) / 2 = 5
- yₘ = (4 + 10) / 2 = 7
Therefore, the coordinates of the midpoint B are (5, 7).
Problem: Given triangle ABC with vertices A(1,2), B(5,4), and C(3,6). Find the coordinates of the midpoint of AB, denoted as D, and verify that the line segment connecting D to the midpoint of BC is parallel to AC and half its length.
Solution:
-
Find the midpoint D of AB: Using the midpoint formula, D = ((1+5)/2, (2+4)/2) = (3,3)
-
Find the midpoint E of BC: Using the midpoint formula, E = ((5+3)/2, (4+6)/2) = (4,5)
-
Find the vector DE: DE = E - D = (4-3, 5-3) = (1,2)
-
Find the vector AC: AC = C - A = (3-1, 6-2) = (2,4)
-
Verify parallelism: Notice that DE = (1/2)AC. This demonstrates that DE is parallel to AC and half its length, confirming the midpoint theorem.
Conclusion: The Ubiquity of Midpoints
The concept of the midpoint, while seemingly simple, is a cornerstone of various mathematical and practical applications. From fundamental geometric principles to advanced computational techniques, the midpoint plays a crucial role in shaping our understanding and solving problems in numerous fields. This article has only scratched the surface; further exploration will reveal even more of its rich and diverse implications within mathematics and beyond. Mastering the midpoint formula and its associated theorems will equip you with a valuable toolset for tackling a wide range of mathematical and real-world challenges. Understanding midpoints is essential for anyone aspiring to a strong foundation in mathematics and its applications.
Latest Posts
Related Post
Thank you for visiting our website which covers about Point B Is The Midpoint Of Ac . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.