Points Of Concurrency In A Triangle
News Co
Apr 07, 2025 · 6 min read
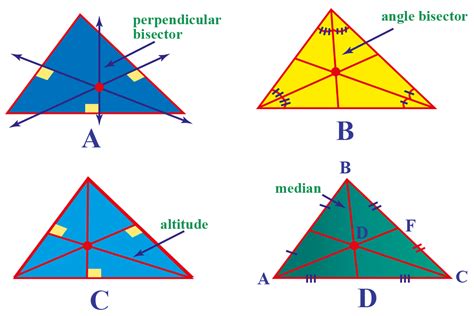
Table of Contents
Points of Concurrency in a Triangle: A Comprehensive Guide
Triangles, the fundamental building blocks of geometry, possess fascinating properties beyond their basic angles and sides. One particularly intriguing aspect lies in their points of concurrency. These are points where multiple significant lines within a triangle intersect, creating a rich tapestry of geometric relationships. Understanding these points of concurrency is crucial for anyone delving deeper into geometry, from high school students to advanced mathematicians. This comprehensive guide will explore the four most prominent points of concurrency: the centroid, circumcenter, incenter, and orthocenter, providing detailed explanations, constructions, and real-world applications.
1. The Centroid: The Triangle's Center of Mass
The centroid of a triangle, often denoted by G, is the point where the three medians of the triangle intersect. A median is a line segment joining a vertex of the triangle to the midpoint of the opposite side. The centroid is also known as the center of mass or geometric center of the triangle. This means that if you were to cut a triangle out of a uniform material, the centroid is the point where the triangle would perfectly balance.
Constructing the Centroid:
- Identify the midpoints: Find the midpoints of each side of the triangle.
- Draw the medians: Draw a line segment from each vertex to the midpoint of the opposite side.
- Point of intersection: The point where these three medians intersect is the centroid.
Properties of the Centroid:
- Dividing medians: The centroid divides each median into a ratio of 2:1. The segment from the vertex to the centroid is twice the length of the segment from the centroid to the midpoint of the opposite side. This is a crucial property often used in coordinate geometry problems.
- Center of mass: As mentioned earlier, the centroid represents the center of mass of a triangle. This is particularly useful in physics and engineering applications.
- Coordinates: If the vertices of a triangle have coordinates (x₁, y₁), (x₂, y₂), and (x₃, y₃), the coordinates of the centroid (G) are given by: G = ((x₁ + x₂ + x₃)/3, (y₁ + y₂ + y₃)/3)
2. The Circumcenter: The Center of the Circumscribed Circle
The circumcenter, denoted by O, is the point where the three perpendicular bisectors of the sides of a triangle intersect. A perpendicular bisector is a line that is perpendicular to a side and passes through its midpoint. The circumcenter is equidistant from all three vertices of the triangle. This means that a circle can be drawn passing through all three vertices, with the circumcenter as its center. This circle is known as the circumcircle.
Constructing the Circumcenter:
- Find midpoints: Locate the midpoint of each side of the triangle.
- Construct perpendicular bisectors: Draw a line perpendicular to each side, passing through its midpoint.
- Point of intersection: The point where these three perpendicular bisectors intersect is the circumcenter.
Properties of the Circumcenter:
- Equidistant from vertices: The circumcenter is equidistant from all three vertices of the triangle. This distance is the radius of the circumcircle.
- Circumcircle: The circumcircle passes through all three vertices of the triangle.
- Acute, obtuse, and right triangles: The location of the circumcenter varies depending on the type of triangle:
- Acute triangle: The circumcenter lies inside the triangle.
- Obtuse triangle: The circumcenter lies outside the triangle.
- Right triangle: The circumcenter lies on the hypotenuse (the midpoint of the hypotenuse).
3. The Incenter: The Center of the Inscribed Circle
The incenter, denoted by I, is the point where the three angle bisectors of the triangle intersect. An angle bisector is a line that divides an angle into two equal angles. The incenter is equidistant from all three sides of the triangle. This means that a circle can be drawn tangent to all three sides, with the incenter as its center. This circle is called the incircle.
Constructing the Incenter:
- Draw angle bisectors: Construct the angle bisector of each angle of the triangle.
- Point of intersection: The point where these three angle bisectors intersect is the incenter.
Properties of the Incenter:
- Equidistant from sides: The incenter is equidistant from all three sides of the triangle. This distance is the radius of the incircle.
- Incircle: The incircle is tangent to all three sides of the triangle.
- Relationship to area: The area of the triangle can be expressed in terms of the inradius (r) and the semi-perimeter (s) using the formula: Area = rs.
4. The Orthocenter: The Intersection of Altitudes
The orthocenter, denoted by H, is the point where the three altitudes of the triangle intersect. An altitude is a line segment from a vertex perpendicular to the opposite side (or its extension). Unlike the other three points of concurrency, the orthocenter's position relative to the triangle is less predictable.
Constructing the Orthocenter:
- Draw altitudes: Draw a line segment from each vertex perpendicular to the opposite side.
- Point of intersection: The point where these three altitudes intersect is the orthocenter.
Properties of the Orthocenter:
- Acute, obtuse, and right triangles: The location of the orthocenter varies depending on the type of triangle:
- Acute triangle: The orthocenter lies inside the triangle.
- Obtuse triangle: The orthocenter lies outside the triangle.
- Right triangle: The orthocenter coincides with the right-angled vertex.
- Euler line: In any triangle that is not equilateral, the centroid, circumcenter, and orthocenter are collinear. This line is known as the Euler line.
Relationships Between the Points of Concurrency
The four points of concurrency—centroid, circumcenter, incenter, and orthocenter—are not independent of each other. Their relative positions within the triangle, particularly in non-equilateral triangles, reveal interesting geometric relationships. The most significant relationship is the Euler line, which connects the centroid, circumcenter, and orthocenter. The centroid divides the segment connecting the circumcenter and orthocenter in a 2:1 ratio.
Applications of Points of Concurrency
The concepts of points of concurrency extend beyond theoretical geometry, finding practical applications in various fields:
- Engineering and Design: The centroid is crucial in determining the center of mass for structural stability calculations in architecture and engineering.
- Computer Graphics: Understanding these points helps in creating realistic 3D models and simulations. For example, the circumcenter is essential for defining the bounding circle around a triangular object.
- Navigation and Surveying: Techniques involving triangulation use the properties of points of concurrency to determine locations and distances.
- Physics: The centroid's role in representing the center of mass is fundamental in physics problems involving balance and equilibrium.
Conclusion
The points of concurrency within a triangle – the centroid, circumcenter, incenter, and orthocenter – represent a rich area of study in geometry. Their properties and interrelationships offer a deeper understanding of triangular geometry, extending beyond basic definitions and into more complex applications across various disciplines. From constructing these points using geometric tools to applying their properties in practical scenarios, a thorough grasp of these concepts enhances geometric intuition and problem-solving skills. Further exploration into these fascinating aspects of triangular geometry can unlock a world of mathematical discovery.
Latest Posts
Related Post
Thank you for visiting our website which covers about Points Of Concurrency In A Triangle . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.