Rational Numbers Vs Irrational Numbers Worksheets
News Co
Apr 05, 2025 · 5 min read
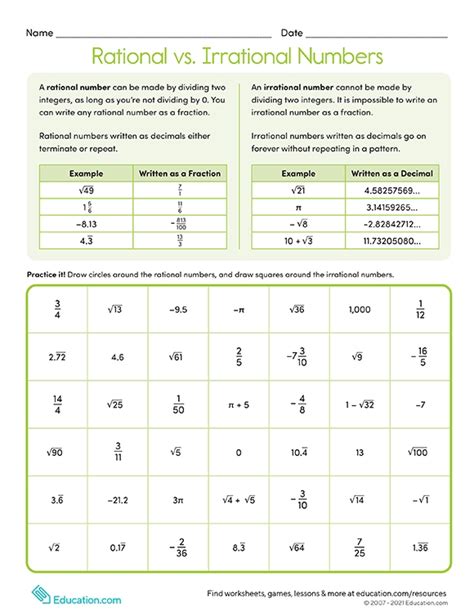
Table of Contents
Rational Numbers vs. Irrational Numbers Worksheets: A Comprehensive Guide for Students
Understanding the difference between rational and irrational numbers is a cornerstone of mathematical proficiency. This comprehensive guide provides a detailed explanation of both rational and irrational numbers, along with various worksheet ideas to solidify student understanding. We'll delve into the definitions, examples, and practical applications, ultimately equipping you with the resources to create effective and engaging worksheets.
What are Rational Numbers?
Rational numbers are numbers that can be expressed as a fraction p/q, where 'p' and 'q' are integers, and 'q' is not equal to zero. This seemingly simple definition encompasses a wide range of numbers.
Examples of Rational Numbers:
- Integers: All whole numbers (positive, negative, and zero) are rational. For example, 5 can be written as 5/1, -3 as -3/1, and 0 as 0/1.
- Fractions: Any number that can be expressed as a fraction, like 1/2, 3/4, -2/5, etc., is a rational number.
- Terminating Decimals: Decimals that end after a finite number of digits are rational. For example, 0.75 (which is 3/4), 2.5 (which is 5/2), and 0.125 (which is 1/8).
- Repeating Decimals: Decimals that have a repeating pattern of digits are also rational. For instance, 0.333... (which is 1/3), 0.666... (which is 2/3), and 0.142857142857... (which is 1/7).
Identifying Rational Numbers on Worksheets:
Worksheets focusing on rational numbers should include a variety of exercises to test understanding. These can include:
- Identifying rational numbers from a list: Students identify which numbers from a given set are rational. This tests their foundational understanding of the definition.
- Converting fractions to decimals: Converting fractions to their decimal equivalents helps students visualize the relationship between the two forms.
- Converting decimals to fractions: The reverse process reinforces their understanding of how fractions and decimals represent the same values.
- Expressing rational numbers in different forms: Students practice writing rational numbers as fractions, decimals, and integers where possible. This emphasizes the versatility of rational numbers.
- Word problems involving rational numbers: Contextualizing rational numbers within real-world problems enhances understanding and application. Examples could involve dividing a pizza, calculating distances, or sharing resources.
What are Irrational Numbers?
Irrational numbers are numbers that cannot be expressed as a fraction p/q, where 'p' and 'q' are integers, and 'q' is not zero. They are non-repeating and non-terminating decimals.
Examples of Irrational Numbers:
- √2: The square root of 2 is a classic example. Its decimal representation goes on forever without repeating: 1.41421356...
- √3: Similarly, the square root of 3 is irrational: 1.7320508...
- √5: The square root of 5 is another example: 2.2360679...
- π (Pi): The ratio of a circle's circumference to its diameter, approximately 3.14159... It's an irrational number that goes on forever without a repeating pattern.
- e (Euler's number): The base of the natural logarithm, approximately 2.71828... Like π, it's an irrational number with an infinite, non-repeating decimal expansion.
Identifying Irrational Numbers on Worksheets:
Worksheets focusing on irrational numbers should challenge students' understanding of infinite, non-repeating decimals. These can include:
- Identifying irrational numbers from a list: Similar to the rational number exercise, this tests their understanding of the definition.
- Approximating irrational numbers: Since irrational numbers cannot be expressed exactly, students can practice approximating their values to a given number of decimal places.
- Understanding the concept of non-repeating, non-terminating decimals: Exercises focusing on this concept help students grasp the core characteristic of irrational numbers.
- Comparing and ordering irrational numbers: Students can practice ordering irrational numbers based on their approximate values.
- Real-world applications of irrational numbers: This includes examples like calculating the circumference or area of a circle using π.
Combining Rational and Irrational Numbers in Worksheets
More advanced worksheets should combine both rational and irrational numbers, forcing students to discriminate between the two.
Worksheet Ideas:
- Classifying numbers: Present a list of numbers and ask students to classify each as rational or irrational, justifying their answers.
- Operations with rational and irrational numbers: Explore addition, subtraction, multiplication, and division involving both rational and irrational numbers. Students should understand that adding a rational and irrational number always results in an irrational number.
- Number line activities: Place numbers (both rational and irrational) on a number line, requiring students to order them correctly. This visually reinforces their understanding of number magnitude.
- Problem-solving scenarios: Present real-world problems that require students to identify and utilize rational and irrational numbers.
Advanced Concepts and Worksheet Extensions
As students become more comfortable, introduce more complex concepts:
- Proofs of irrationality: Introduce simple proofs, such as proving the irrationality of √2, to challenge advanced students and develop critical thinking skills.
- Decimal expansions and their relationship to rationality: Delve deeper into the relationship between the nature of a decimal expansion (terminating, repeating, or non-repeating) and whether the number is rational or irrational.
- Sets and subsets: Introduce set notation and discuss the relationship between the sets of rational numbers (ℚ) and irrational numbers (the set of irrational numbers doesn't have a standard symbol, often denoted as ℝ \ ℚ, where ℝ represents real numbers).
- Real numbers: Explain that rational and irrational numbers together form the set of real numbers.
Creating Engaging Worksheets: Tips and Tricks
- Variety is key: Include diverse problem types to avoid monotony.
- Gradual progression: Start with simpler exercises and gradually increase the difficulty level.
- Clear instructions: Provide clear and concise instructions for each exercise.
- Visual aids: Use diagrams, graphs, and number lines to enhance understanding.
- Real-world contexts: Connect the concepts to real-world situations to make learning more relevant.
- Use technology: Explore online tools and platforms to generate customized worksheets.
- Include answer keys: Provide answer keys to allow students to self-check their work and identify areas for improvement.
- Feedback and review: Encourage students to review their answers and seek clarification when needed.
Conclusion
Mastering the distinction between rational and irrational numbers is essential for mathematical growth. By utilizing diverse worksheet types that incorporate the concepts explained above, educators can effectively solidify students' understanding and build a strong foundation for advanced mathematical studies. Remember to tailor the difficulty and content to the students' level, fostering a learning environment that promotes both understanding and enjoyment. Through consistent practice and creative worksheet design, students will confidently navigate the world of rational and irrational numbers.
Latest Posts
Related Post
Thank you for visiting our website which covers about Rational Numbers Vs Irrational Numbers Worksheets . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.