Same Side Interior Angles Are Supplementary
News Co
Apr 03, 2025 · 6 min read
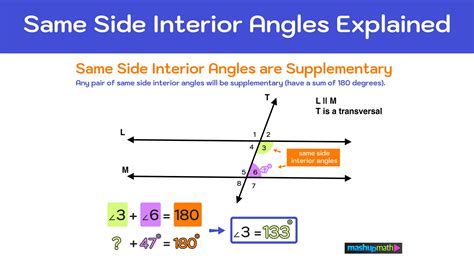
Table of Contents
Same-Side Interior Angles Are Supplementary: A Deep Dive into Geometry
Geometry, the study of shapes, sizes, relative positions of figures, and the properties of space, often presents concepts that, while seemingly simple at first glance, reveal intricate layers of understanding upon closer examination. One such concept is the relationship between same-side interior angles, specifically, their supplementary nature. This article delves deep into this geometric principle, exploring its definition, proof, applications, and real-world examples, equipping you with a comprehensive understanding.
Understanding Same-Side Interior Angles
Before we delve into the supplementary relationship, let's define our key players: same-side interior angles. Consider two parallel lines intersected by a transversal line. A transversal is simply a line that intersects two or more other lines at distinct points. This intersection creates eight angles. Same-side interior angles are a specific pair of these angles.
They are located inside the parallel lines and on the same side of the transversal. They are not adjacent angles; they are separated by the transversal.
Key Characteristics:
- Location: Inside the parallel lines.
- Side: On the same side of the transversal.
- Non-adjacency: Not directly next to each other.
Think of it like this: Imagine two parallel train tracks intersected by a road. The angles formed inside the tracks, on the same side of the road, represent same-side interior angles.
Visual Representation
[Imagine a diagram here showing two parallel lines, l and m, intersected by transversal line t. Clearly label the same-side interior angles, perhaps using angle notation like ∠1 and ∠2.]
This visual representation helps solidify the concept. You can easily identify the same-side interior angle pairs in any diagram involving parallel lines and a transversal.
The Supplementary Relationship: Proof and Explanation
The core principle we're exploring is that same-side interior angles are supplementary. This means that their measures add up to 180 degrees. But why is this true? Let's explore the proof.
Proof using Corresponding Angles:
-
Corresponding Angles are Congruent: We begin by recognizing that when parallel lines are intersected by a transversal, corresponding angles are congruent. Corresponding angles are angles that occupy the same relative position at an intersection when a line intersects two other lines. If you look at the diagram, you'll see several pairs of corresponding angles.
-
Linear Pair are Supplementary: A linear pair of angles are adjacent angles that form a straight line, meaning they add up to 180 degrees. Notice that one of the same-side interior angles forms a linear pair with a corresponding angle to the other same-side interior angle.
-
Substitution: Since corresponding angles are congruent, we can substitute the measure of one same-side interior angle with its corresponding angle in the linear pair equation.
-
Conclusion: This substitution demonstrates that the sum of the measures of the same-side interior angles equals 180 degrees, proving that they are supplementary.
Proof using Alternate Interior Angles:
Another approach uses alternate interior angles. Alternate interior angles are angles that lie on opposite sides of the transversal and inside the parallel lines. These angles are also congruent.
-
Alternate Interior Angles are Congruent: Identify a pair of alternate interior angles.
-
Supplementary Angles: Observe that the other same-side interior angle forms a linear pair with one of the alternate interior angles.
-
Substitution and Conclusion: Similar to the previous proof, substituting the congruent alternate interior angles demonstrates that the sum of the same-side interior angles is 180 degrees.
Applications and Real-World Examples
The concept of same-side interior angles being supplementary is not merely a theoretical concept; it has significant practical applications in various fields:
1. Construction and Engineering:
Imagine building a bridge or constructing a skyscraper. Ensuring that parallel beams or supports are properly aligned is critical for structural integrity. The principle of same-side interior angles allows engineers and architects to accurately measure and verify the angles, guaranteeing stability and preventing structural failures. By understanding the relationship between the angles formed, they can make precise calculations for constructing parallel structures, leading to safe and stable buildings and infrastructure.
2. Navigation and Surveying:
Surveying and navigation rely heavily on geometric principles. Determining distances and directions often involves establishing parallel lines (e.g., using a compass or GPS coordinates) and measuring angles. Understanding same-side interior angles helps in accurate calculations for determining the location, distance, and orientation of objects or points. The principle can enhance accuracy in mapping and creating accurate geographical representations.
3. Computer Graphics and Game Development:
In the realm of computer graphics and game development, the placement and orientation of objects within a virtual world are critical. This principle is fundamental in creating realistic 3D environments and ensuring objects align correctly. Consider the rendering of parallel roads or railway lines in a video game: the accurate representation of angles formed by intersecting lines, using the concept of same-side interior angles, guarantees realism and avoids visual distortions.
4. Design and Architecture:
In design and architecture, parallel lines and angles are often used for aesthetic purposes and to create visual balance. The concept of same-side interior angles can be utilized to ensure that these parallel lines are properly aligned and visually consistent. Understanding this relationship aids architects in creating aesthetically pleasing and structurally sound designs.
Problem Solving and Practice
Let's reinforce our understanding with some example problems:
Problem 1:
Two parallel lines are intersected by a transversal. One same-side interior angle measures 110 degrees. What is the measure of the other same-side interior angle?
Solution: Since same-side interior angles are supplementary, their sum is 180 degrees. Therefore, the other angle measures 180 - 110 = 70 degrees.
Problem 2:
Two parallel lines are intersected by a transversal. One same-side interior angle is represented by the expression 3x + 20, and the other by 2x + 40. Find the value of x and the measure of each angle.
Solution: Set up the equation 3x + 20 + 2x + 40 = 180. Solving for x gives x = 24. Substituting x back into the expressions gives the angles as 92 degrees and 88 degrees.
Advanced Concepts and Extensions
While this article primarily focuses on the fundamental concept, it's important to note that the supplementary nature of same-side interior angles extends to more complex geometric scenarios:
-
Non-parallel lines: While the principle is most clearly demonstrated with parallel lines, the relationship between angles changes when the lines are not parallel. The sum of same-side interior angles will be different from 180 degrees and will depend on the angle between the non-parallel lines.
-
Multiple transversals: When multiple transversals intersect a pair of parallel lines, the same-side interior angles formed by each transversal will still be supplementary. However, different transversals will create different sets of supplementary angles.
-
Three-dimensional geometry: The concept extends to three-dimensional space where parallel planes are intersected by other planes. The principle remains the same, with supplementary relationships observed between the analogous angles.
Conclusion
The concept of same-side interior angles being supplementary is a cornerstone of geometry, providing a powerful tool for solving problems in various fields. From construction to computer graphics, the understanding of this principle ensures accuracy, precision, and structural integrity. By mastering this concept, and practicing solving problems, you'll gain a deeper appreciation for the elegance and practicality of geometric principles. This article has provided a comprehensive exploration of same-side interior angles, moving beyond the basic definition to delve into the proof, applications, and advanced considerations. Through a step-by-step approach, enriched by practical examples and exercises, this resource empowers readers to confidently grasp this pivotal concept in geometry.
Latest Posts
Latest Posts
-
What Is A Factor Of 92
Apr 04, 2025
-
What Is The Least Common Multiple Of 12 And 8
Apr 04, 2025
-
What Percentage Is 30 Of 50
Apr 04, 2025
-
12 Weeks Is Equal To How Many Months
Apr 04, 2025
-
What Are The Factors Of 86
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about Same Side Interior Angles Are Supplementary . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
