Second Derivative Of X Ln X
News Co
Mar 23, 2025 · 5 min read
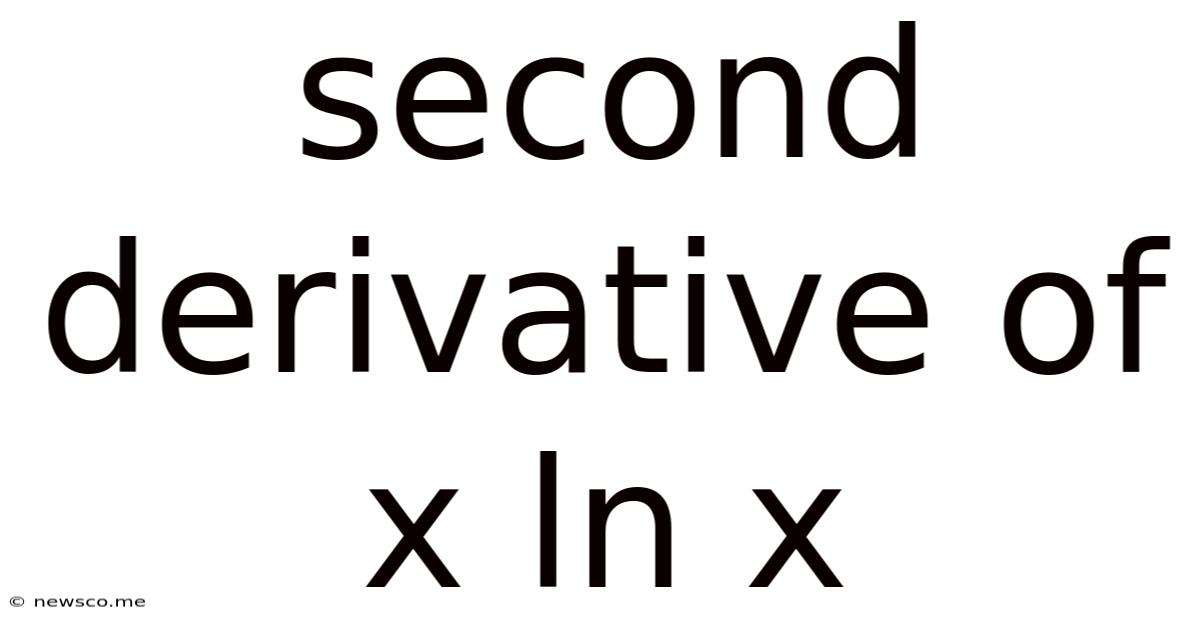
Table of Contents
Delving Deep: A Comprehensive Exploration of the Second Derivative of x ln x
The seemingly simple function, x ln x, holds a surprising depth when we delve into its higher-order derivatives. This article provides a comprehensive exploration of the second derivative of x ln x, examining its derivation, properties, and applications. We'll move beyond the simple calculation to understand the underlying mathematical concepts and their significance.
Understanding the First Derivative
Before tackling the second derivative, we must first solidify our understanding of the first derivative. This step is crucial, as the second derivative builds directly upon the first.
The function we're analyzing is f(x) = x ln x. To find its first derivative, we employ the product rule of differentiation, which states that the derivative of a product of two functions is the derivative of the first function times the second function plus the first function times the derivative of the second function.
Mathematically, if we have two functions, u(x) and v(x), then the derivative of their product is:
(uv)' = u'v + uv'
In our case, u(x) = x and v(x) = ln x. Therefore:
- u'(x) = 1 (the derivative of x with respect to x)
- v'(x) = 1/x (the derivative of ln x with respect to x)
Applying the product rule:
f'(x) = (1)(ln x) + (x)(1/x) = ln x + 1
Therefore, the first derivative of x ln x is ln x + 1.
Deriving the Second Derivative
Now, the exciting part: finding the second derivative. The second derivative is simply the derivative of the first derivative. In other words, we need to differentiate f'(x) = ln x + 1.
This time, we'll use a straightforward approach. The derivative of a sum is the sum of the derivatives. Thus:
f''(x) = d/dx (ln x + 1) = d/dx (ln x) + d/dx (1)
The derivative of 1 (a constant) with respect to x is 0. The derivative of ln x with respect to x is 1/x.
Therefore, the second derivative of x ln x is f''(x) = 1/x.
Properties and Analysis of the Second Derivative
The second derivative, 1/x, reveals several interesting properties:
-
Asymptotic Behavior: As x approaches infinity, the second derivative approaches 0. This signifies that the rate of change of the slope of the original function decreases as x gets larger.
-
Undefined at x = 0: The second derivative is undefined at x = 0. This point is significant because the original function x ln x itself is also undefined at x = 0. This is due to the nature of the natural logarithm, which is undefined for non-positive values.
-
Sign Change: The second derivative changes sign at x = 0. For x > 0, the second derivative is positive, indicating that the original function is concave up (convex). For x < 0, the second derivative would be negative (assuming we were considering complex numbers, as the natural log is undefined in the real domain for negative numbers), suggesting concave down (concave).
-
Relationship to Concavity: The second derivative is a powerful tool for determining the concavity of a function. A positive second derivative indicates concavity upwards (a "U" shape), while a negative second derivative indicates concavity downwards (an inverted "U" shape). In our case, for positive x values, the positive second derivative confirms the convex nature of the function x ln x.
Applications and Significance
The second derivative, and indeed higher-order derivatives, find numerous applications in various fields:
-
Physics: In physics, the second derivative is used extensively. For example, in classical mechanics, the second derivative of position with respect to time represents acceleration.
-
Economics: In economics, second derivatives are crucial in analyzing marginal cost and marginal revenue functions. They help determine whether a function is increasing at an increasing or decreasing rate.
-
Optimization Problems: Finding the maximum or minimum of a function often involves examining the second derivative. If the second derivative is positive at a critical point, the function has a local minimum; if it's negative, it has a local maximum. The second derivative test helps us distinguish between these.
-
Curve Sketching: The second derivative provides valuable insight into the shape of a curve. By analyzing the sign of the second derivative, we can determine the concavity of the function and identify inflection points, where the concavity changes.
Extending the Analysis: Higher-Order Derivatives
While we've focused on the second derivative, it's insightful to consider higher-order derivatives. Let's find the third derivative:
f'''(x) = d/dx (1/x) = d/dx (x⁻¹) = -x⁻² = -1/x²
The third derivative is -1/x². Notice that it's always negative for positive x values.
Continuing this pattern, the nth derivative can be expressed as:
f⁽ⁿ⁾(x) = (-1)ⁿ⁻¹ (n-1)! / xⁿ
This formula demonstrates a clear pattern in the higher-order derivatives of x ln x.
Practical Implications and Real-World Connections
The concept of the second derivative, seemingly abstract, has tangible real-world consequences. Understanding concavity, as determined by the second derivative, is vital in numerous engineering applications. For example, structural engineers use this principle to design structures that can withstand stress and deformation. The shape of a bridge, for instance, is optimized considering the principles of curvature and concavity to ensure stability and safety.
Similarly, in manufacturing processes, understanding the rate of change of the rate of change (the second derivative) is essential for optimizing production efficiency and minimizing waste. Optimizing processes often involves identifying inflection points, which indicate a change in the rate of improvement.
Conclusion: Beyond the Calculus
This in-depth analysis of the second derivative of x ln x transcends a simple calculation. It demonstrates the power and elegance of calculus in unraveling the intricate properties of functions. By understanding the second derivative, we gain a deeper understanding not just of the mathematical properties of the function, but also its real-world implications across diverse fields. The analysis extends beyond the immediate calculation to encompass the broader concepts of concavity, optimization, and the power of higher-order derivatives in providing insightful information about the behavior of a function. This comprehensive exploration underscores the importance of mathematical analysis in providing a robust framework for understanding and interpreting the world around us. Furthermore, it highlights the interconnectedness of seemingly disparate fields, revealing the underlying mathematical principles that govern various aspects of our world.
Latest Posts
Related Post
Thank you for visiting our website which covers about Second Derivative Of X Ln X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.