Simplest Form Of 75 / 100
News Co
Apr 17, 2025 · 5 min read
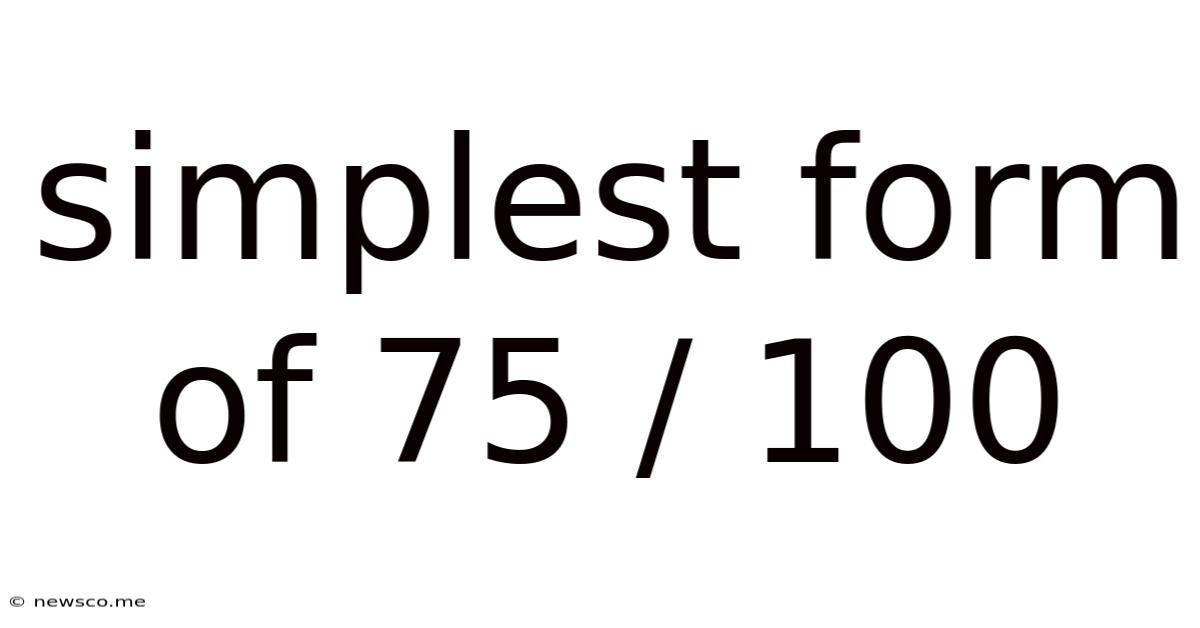
Table of Contents
The Simplest Form of 75/100: A Comprehensive Guide to Fraction Simplification
Finding the simplest form of a fraction is a fundamental concept in mathematics, crucial for various applications from basic arithmetic to advanced calculus. This comprehensive guide will delve into the process of simplifying fractions, using the example of 75/100 to illustrate the steps involved. We will explore different methods, explain the underlying principles, and discuss the importance of simplifying fractions in various mathematical contexts. This guide will also touch upon related concepts like ratios and proportions, enriching your understanding of fraction simplification.
Understanding Fractions
Before we dive into simplifying 75/100, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two main parts:
- Numerator: The top number representing the portion of the whole.
- Denominator: The bottom number indicating the total number of equal parts the whole is divided into.
In the fraction 75/100, 75 is the numerator, and 100 is the denominator. This means we have 75 parts out of a total of 100 equal parts.
Simplifying Fractions: The Core Concept
Simplifying a fraction means expressing it in its lowest terms. This means finding an equivalent fraction where the numerator and denominator have no common factors other than 1. The simplified fraction represents the same value as the original fraction but in a more concise and manageable form. This is essential for easier calculations and clearer understanding.
Methods for Simplifying Fractions
There are several ways to simplify a fraction. Let's explore the most common methods, applying them to 75/100:
Method 1: Finding the Greatest Common Divisor (GCD)
This method is considered the most efficient way to simplify fractions. The GCD, also known as the greatest common factor (GCF), is the largest number that divides both the numerator and denominator without leaving a remainder.
-
Find the factors of the numerator (75): 1, 3, 5, 15, 25, 75
-
Find the factors of the denominator (100): 1, 2, 4, 5, 10, 20, 25, 50, 100
-
Identify the greatest common factor: The largest number that appears in both lists is 25.
-
Divide both the numerator and denominator by the GCD:
75 ÷ 25 = 3 100 ÷ 25 = 4
Therefore, the simplest form of 75/100 is 3/4.
Method 2: Repeated Division by Common Factors
This method involves repeatedly dividing the numerator and denominator by their common factors until no common factors remain.
-
Identify a common factor: Both 75 and 100 are divisible by 5.
-
Divide both by 5:
75 ÷ 5 = 15 100 ÷ 5 = 20
-
Check for further common factors: Both 15 and 20 are divisible by 5.
-
Divide both by 5 again:
15 ÷ 5 = 3 20 ÷ 5 = 4
Now, we have 3/4, and there are no more common factors. Thus, the simplest form of 75/100 is 3/4.
Method 3: Prime Factorization
This method involves expressing the numerator and denominator as products of their prime factors. A prime number is a number greater than 1 that has only two factors: 1 and itself.
-
Find the prime factorization of 75: 3 x 5 x 5 = 3 x 5²
-
Find the prime factorization of 100: 2 x 2 x 5 x 5 = 2² x 5²
-
Identify common prime factors: Both factorizations contain 5².
-
Cancel out the common factors: This leaves us with 3/ (2²) which simplifies to 3/4.
Therefore, the simplest form of 75/100 is 3/4.
Why Simplify Fractions?
Simplifying fractions offers several advantages:
- Easier Calculations: Simplified fractions make calculations significantly easier. For instance, adding 3/4 and 1/4 is much simpler than adding 75/100 and 25/100.
- Clearer Understanding: A simplified fraction provides a clearer representation of the portion of the whole. 3/4 is more readily understood than 75/100.
- Improved Communication: Using simplified fractions improves the clarity and efficiency of mathematical communication.
- Applications in various fields: Fraction simplification is fundamental in various fields like engineering, physics, and computer science where precise calculations are crucial.
Fractions, Ratios, and Proportions
The concept of fraction simplification is closely related to ratios and proportions. A ratio compares two or more quantities, while a proportion is a statement that equates two ratios.
For example, the ratio 75:100 is equivalent to the ratio 3:4, which is obtained by simplifying the fraction 75/100. This simplification is essential for solving proportion problems and understanding relationships between quantities.
Practical Applications of Fraction Simplification
The skill of simplifying fractions extends beyond the realm of theoretical mathematics. It has practical applications in everyday life, including:
- Cooking and Baking: Following recipes often requires adjusting ingredient quantities, which necessitates simplifying fractions.
- Construction and Engineering: Precise measurements and calculations in construction and engineering rely heavily on fraction simplification.
- Finance and Accounting: Calculating percentages, interest rates, and proportions in financial contexts often requires manipulating fractions.
- Data Analysis: Simplifying fractions helps in interpreting and representing data more effectively.
Conclusion
Simplifying fractions, as demonstrated through the example of 75/100, is a crucial skill in mathematics with far-reaching applications. Mastering different methods, such as finding the GCD, repeated division, and prime factorization, allows for efficient and accurate simplification. Understanding the reasons behind simplification – easier calculations, clearer understanding, and improved communication – solidifies its importance in both academic and practical contexts. Furthermore, the connection between fraction simplification and ratios and proportions highlights its broader significance within the field of mathematics and its applications in various real-world scenarios. The ability to effortlessly simplify fractions is a cornerstone of mathematical fluency, contributing to a more profound grasp of numerical relationships and problem-solving abilities. Practice is key; the more you work with fractions, the more intuitive and effortless the simplification process will become.
Latest Posts
Related Post
Thank you for visiting our website which covers about Simplest Form Of 75 / 100 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.