Simplify X 2 X 2 1
News Co
Apr 18, 2025 · 5 min read
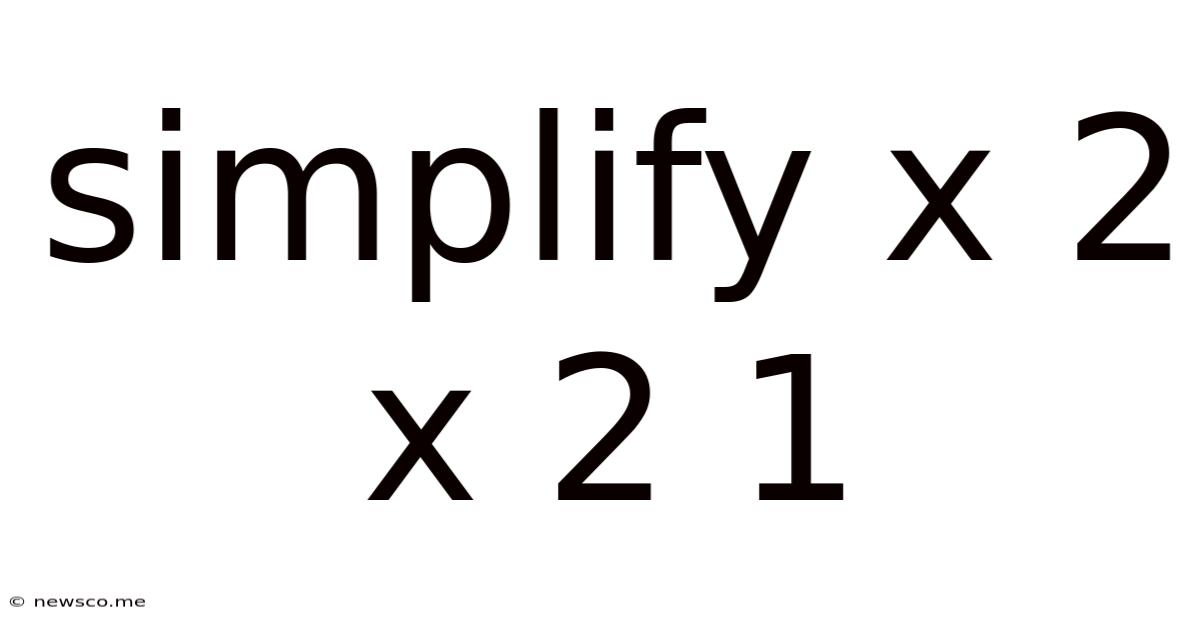
Table of Contents
Simplify x² + 2x + 1: A Comprehensive Guide
Quadratic expressions are fundamental building blocks in algebra. Understanding how to simplify and manipulate them is crucial for success in mathematics and related fields. This article delves into the simplification of the expression x² + 2x + 1, exploring various methods, their applications, and the underlying mathematical concepts. We'll move beyond the simple solution to provide a deeper understanding of the topic, enriching your algebraic toolkit.
Understanding the Expression x² + 2x + 1
The expression x² + 2x + 1 is a quadratic trinomial, meaning it's a polynomial with three terms, the highest power of the variable (x) being 2. This particular trinomial is a special case – a perfect square trinomial. This special characteristic allows for simplification techniques not applicable to all quadratic expressions. Recognizing this pattern is a key step in efficiently simplifying the expression.
Method 1: Factoring the Perfect Square Trinomial
The most efficient way to simplify x² + 2x + 1 is by recognizing it as a perfect square trinomial and factoring it. A perfect square trinomial is a trinomial that can be factored into the square of a binomial. The general form of a perfect square trinomial is:
a² + 2ab + b² = (a + b)²
or
a² - 2ab + b² = (a - b)²
In our case, x² + 2x + 1 fits the first form:
- a² = x² (a = x)
- 2ab = 2x (2 * x * 1 = 2x, so b = 1)
- b² = 1 (b = 1)
Therefore, x² + 2x + 1 can be factored as:
(x + 1)²
This is the simplest form of the expression. This method relies on pattern recognition and understanding the properties of perfect square trinomials.
Method 2: Completing the Square
Completing the square is a more general technique used to solve quadratic equations and simplify quadratic expressions. It's particularly useful when factoring isn't immediately obvious. Let's apply it to x² + 2x + 1:
-
Identify the coefficient of x: The coefficient of x is 2.
-
Divide the coefficient by 2: 2 / 2 = 1
-
Square the result: 1² = 1
-
Add and subtract the result: We add and subtract 1 to the expression without changing its value:
x² + 2x + 1 - 1
-
Factor the perfect square trinomial: The first three terms (x² + 2x + 1) form a perfect square trinomial, which we can factor as (x + 1)².
-
Simplify: The expression becomes:
(x + 1)² - 1 + 1 = (x + 1)²
This method demonstrates that completing the square leads to the same simplified form: (x + 1)². This method is valuable for more complex quadratic expressions where factoring might be challenging.
Method 3: Using the Quadratic Formula (Less Efficient in this Case)
While the quadratic formula is a powerful tool for solving quadratic equations, it's less efficient for simplifying expressions like x² + 2x + 1. The quadratic formula is:
x = [-b ± √(b² - 4ac)] / 2a
where a, b, and c are the coefficients of the quadratic equation ax² + bx + c = 0.
In our case, a = 1, b = 2, and c = 1. However, applying the quadratic formula here would be an unnecessarily complex approach compared to factoring or completing the square. The quadratic formula provides the roots of the equation, not a simplified form of the expression itself.
Applications of Simplified Expressions
The simplified form, (x + 1)², has numerous applications in various mathematical contexts:
-
Solving Quadratic Equations: If x² + 2x + 1 = 0, then (x + 1)² = 0, which implies x = -1. This shows the power of simplification in solving equations.
-
Calculus: In calculus, simplifying expressions is crucial for differentiation and integration. The simplified form is easier to manipulate during these operations.
-
Geometry: Quadratic expressions often appear in geometric problems involving areas and volumes. Simplifying these expressions helps in solving for unknown dimensions.
-
Physics and Engineering: Numerous physical phenomena are modeled using quadratic equations. Simplifying these expressions helps in analyzing and predicting system behavior.
-
Computer Science: Quadratic equations and expressions are fundamental in algorithms and data structures, particularly those related to optimization and search problems.
Expanding the Understanding: Beyond x² + 2x + 1
While we've focused on x² + 2x + 1, the principles discussed apply to a broader range of quadratic expressions. Let's explore some variations:
-
Variations in Coefficients: Consider expressions like 4x² + 4x + 1 or 9x² + 6x + 1. These are also perfect square trinomials and can be factored similarly. The key is recognizing the pattern and extracting the square root of the first and last terms.
-
Expressions with Different Signs: Expressions like x² - 2x + 1 follow the same principles but result in (x - 1)². The sign of the middle term determines the sign within the binomial.
-
More Complex Trinomials: Expressions that aren't perfect square trinomials require different factoring techniques, such as the AC method or grouping. However, the underlying principles of simplification remain relevant. The goal is always to express the expression in its most concise and manageable form.
Advanced Concepts and Further Exploration
For those seeking a deeper understanding, here are some advanced concepts related to quadratic expressions and their simplification:
-
Discriminant: The discriminant (b² - 4ac) reveals information about the nature of the quadratic equation's roots (real, distinct, or complex).
-
Vertex Form: Quadratic expressions can be written in vertex form, which provides insights into the parabola's vertex and axis of symmetry.
-
Polynomial Division: For more complex polynomial expressions, polynomial long division or synthetic division can be used to simplify expressions.
Conclusion: Mastering Quadratic Simplification
Simplifying expressions like x² + 2x + 1 is a fundamental skill in algebra. By mastering the methods of factoring, completing the square, and recognizing patterns, you build a robust foundation for tackling more complex mathematical problems across diverse fields. This article has provided a comprehensive guide, going beyond the simple solution to explore deeper mathematical concepts and applications. Remember, practice is key to developing proficiency in simplifying quadratic expressions. The more you work with these types of problems, the more easily you'll recognize patterns and apply the appropriate methods. The ability to quickly and accurately simplify quadratic expressions is a testament to your mastery of algebraic principles and an essential skill for success in many academic and professional pursuits.
Latest Posts
Related Post
Thank you for visiting our website which covers about Simplify X 2 X 2 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.