Sin 60 Cos 30 - Cos 60 Sin 30
News Co
May 05, 2025 · 5 min read
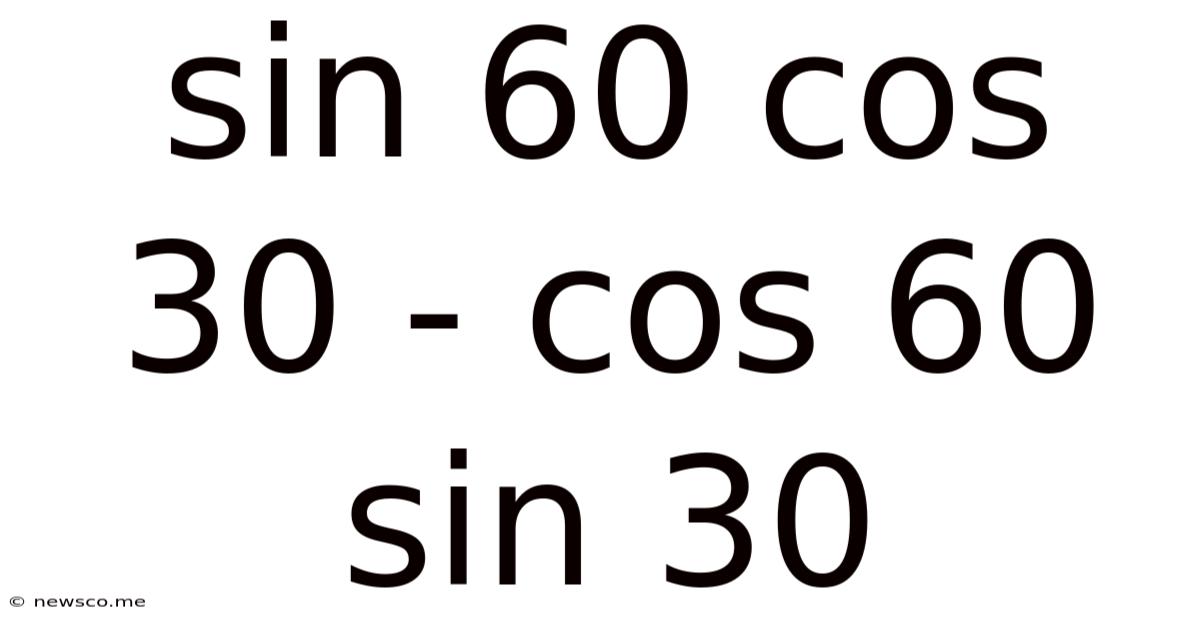
Table of Contents
- Sin 60 Cos 30 - Cos 60 Sin 30
- Table of Contents
- Decoding sin 60 cos 30 - cos 60 sin 30: A Deep Dive into Trigonometric Identities
- Understanding the Fundamentals: Sine, Cosine, and Angles
- Solving sin 60° cos 30° - cos 60° sin 30°
- The Significance of the Result and its Connection to Trigonometric Identities
- Applications of Trigonometric Identities: A Broader Perspective
- 1. Engineering and Physics
- 2. Computer Graphics and Game Development
- 3. Music Theory and Signal Processing
- 4. Navigation and Surveying
- Beyond the Basics: Exploring More Complex Trigonometric Identities
- Conclusion: Mastering Trigonometric Identities for a Deeper Understanding
- Latest Posts
- Related Post
Decoding sin 60 cos 30 - cos 60 sin 30: A Deep Dive into Trigonometric Identities
The expression sin 60° cos 30° - cos 60° sin 30° might seem daunting at first glance, especially to those less familiar with trigonometry. However, understanding this expression unlocks a deeper appreciation for trigonometric identities and their applications in various fields, from engineering and physics to computer graphics and music theory. This article provides a comprehensive exploration of this expression, unraveling its meaning, solving it step-by-step, and demonstrating its broader significance within the world of mathematics.
Understanding the Fundamentals: Sine, Cosine, and Angles
Before delving into the intricacies of the expression, let's refresh our understanding of sine and cosine functions. These are fundamental trigonometric functions that relate the angles of a right-angled triangle to the lengths of its sides.
-
Sine (sin): In a right-angled triangle, the sine of an angle is defined as the ratio of the length of the side opposite the angle to the length of the hypotenuse.
-
Cosine (cos): The cosine of an angle is the ratio of the length of the side adjacent to the angle to the length of the hypotenuse.
The angles in our expression, 30° and 60°, are special angles within trigonometry because their sine and cosine values are easily calculated and often memorized. These values stem from the properties of 30-60-90 triangles, which are special right-angled triangles with a ratio of sides 1:√3:2.
Solving sin 60° cos 30° - cos 60° sin 30°
Now, let's tackle the expression itself: sin 60° cos 30° - cos 60° sin 30°. To solve this, we need to substitute the known values of sin 60°, cos 30°, cos 60°, and sin 30°.
Step 1: Recall the values of sin 30°, cos 30°, sin 60°, and cos 60°
- sin 30° = 1/2
- cos 30° = √3/2
- sin 60° = √3/2
- cos 60° = 1/2
Step 2: Substitute these values into the expression:
sin 60° cos 30° - cos 60° sin 30° = (√3/2) * (√3/2) - (1/2) * (1/2)
Step 3: Perform the multiplication:
(√3/2) * (√3/2) = 3/4 (1/2) * (1/2) = 1/4
Step 4: Complete the subtraction:
3/4 - 1/4 = 2/4
Step 5: Simplify the fraction:
2/4 = 1/2
Therefore, the solution to the expression sin 60° cos 30° - cos 60° sin 30° is 1/2.
The Significance of the Result and its Connection to Trigonometric Identities
This seemingly simple calculation reveals a fundamental trigonometric identity: the difference formula for sine. The general form of this identity is:
sin (A - B) = sin A cos B - cos A sin B
In our expression, A = 60° and B = 30°. Therefore, the expression is equivalent to:
sin (60° - 30°) = sin 30° = 1/2
This demonstrates the power of trigonometric identities in simplifying complex expressions. Instead of performing individual calculations for each trigonometric function, we can use identities to directly arrive at the solution.
Applications of Trigonometric Identities: A Broader Perspective
Trigonometric identities, like the one demonstrated above, are not mere mathematical curiosities; they have wide-ranging applications in various fields. Here are some examples:
1. Engineering and Physics
Trigonometric identities are crucial in solving problems related to:
- Vectors: Representing and manipulating vectors, which are fundamental in physics and engineering, often involves trigonometric functions and their identities.
- Waves: Analyzing wave phenomena, including sound and light waves, requires a strong understanding of trigonometric identities.
- Circuits: In electrical engineering, AC circuit analysis relies heavily on trigonometric functions and identities.
- Mechanics: Problems involving forces, motion, and equilibrium frequently use trigonometric identities for calculations.
2. Computer Graphics and Game Development
Trigonometric functions and identities play a critical role in:
- Rotation and transformation: Objects in computer graphics are manipulated using transformations like rotation and scaling, which often require trigonometric functions.
- 3D modeling: Creating realistic 3D models and animations requires precise calculations involving angles and trigonometric functions.
3. Music Theory and Signal Processing
Trigonometric identities are used in:
- Sound analysis: Analyzing sound waves and understanding musical harmony involves Fourier analysis, which heavily relies on trigonometric functions.
- Signal processing: In fields like telecommunications and audio engineering, signal processing techniques make extensive use of trigonometric identities.
4. Navigation and Surveying
Trigonometric identities are essential for:
- Calculating distances: Surveyors and navigators use trigonometry to calculate distances and locations using angles and measurements.
- Mapping: Creating accurate maps involves trigonometric calculations and identities.
Beyond the Basics: Exploring More Complex Trigonometric Identities
The expression sin 60° cos 30° - cos 60° sin 30° serves as a gateway to a much wider world of trigonometric identities. Understanding this basic identity allows one to tackle more complex identities and problems, such as:
- Sum and difference formulas for cosine: Similar to the sine difference formula, there are corresponding formulas for the cosine function.
- Double angle formulas: These formulas allow us to express trigonometric functions of 2A in terms of trigonometric functions of A.
- Half angle formulas: These identities express trigonometric functions of A/2 in terms of trigonometric functions of A.
- Product-to-sum and sum-to-product formulas: These identities allow us to transform products of trigonometric functions into sums, and vice-versa.
Conclusion: Mastering Trigonometric Identities for a Deeper Understanding
The seemingly simple expression sin 60° cos 30° - cos 60° sin 30° provides a valuable entry point into the world of trigonometric identities. By understanding its solution and the underlying identity it represents, we gain a deeper appreciation for the power and versatility of trigonometry. This knowledge extends far beyond theoretical mathematics, finding practical applications in diverse fields. Mastering these identities unlocks a deeper understanding of mathematical relationships and expands one's ability to solve complex problems across numerous disciplines. The journey of learning trigonometry is a continuous one, and this expression serves as a stepping stone towards more advanced concepts and applications.
Latest Posts
Related Post
Thank you for visiting our website which covers about Sin 60 Cos 30 - Cos 60 Sin 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.