Sin And Cos And Tan Rules
News Co
Apr 05, 2025 · 5 min read
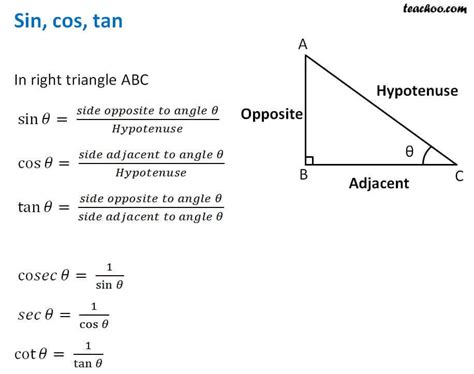
Table of Contents
Sine, Cosine, and Tangent Rules: A Deep Dive into Trigonometry
Trigonometry, a branch of mathematics dealing with the relationships between angles and sides of triangles, forms the backbone of many scientific and engineering disciplines. At its heart lie three fundamental functions: sine (sin), cosine (cos), and tangent (tan). Understanding their rules and applications is crucial for anyone wanting to grasp the power of this mathematical field. This comprehensive guide will explore these functions in detail, covering their definitions, key identities, and practical applications.
Understanding the Basics: Defining Sin, Cos, and Tan
Before diving into the rules, let's establish a clear understanding of the definitions of sine, cosine, and tangent. These functions are typically introduced within the context of a right-angled triangle.
Right-Angled Triangle Fundamentals
A right-angled triangle possesses one angle of 90 degrees (a right angle). The sides opposite to the angles have specific names:
- Hypotenuse: The longest side, always opposite the right angle.
- Opposite: The side opposite to the angle we are considering.
- Adjacent: The side next to the angle we are considering (not the hypotenuse).
Defining the Trigonometric Functions
Using these definitions, we can define sine, cosine, and tangent as follows:
-
Sine (sin θ): The ratio of the length of the side opposite to angle θ to the length of the hypotenuse. sin θ = Opposite / Hypotenuse
-
Cosine (cos θ): The ratio of the length of the side adjacent to angle θ to the length of the hypotenuse. cos θ = Adjacent / Hypotenuse
-
Tangent (tan θ): The ratio of the length of the side opposite to angle θ to the length of the side adjacent to angle θ. tan θ = Opposite / Adjacent
Remember: θ (theta) represents the angle we are interested in.
Key Trigonometric Identities: The Rules of the Game
Trigonometric identities are equations that are true for all values of the angles involved. Mastering these identities is fundamental to simplifying complex trigonometric expressions and solving various problems.
Pythagorean Identity
The Pythagorean identity is arguably the most important trigonometric identity. It stems directly from the Pythagorean theorem for right-angled triangles (a² + b² = c²), where 'a' and 'b' are the legs and 'c' is the hypotenuse. In trigonometric terms, it is expressed as:
sin²θ + cos²θ = 1
This identity holds true for any angle θ.
Reciprocal Identities
These identities relate sine, cosine, and tangent to their reciprocal functions: cosecant (csc), secant (sec), and cotangent (cot), respectively.
- csc θ = 1 / sin θ
- sec θ = 1 / cos θ
- cot θ = 1 / tan θ
Quotient Identities
These identities show the relationship between tangent and cotangent to sine and cosine:
- tan θ = sin θ / cos θ
- cot θ = cos θ / sin θ
Angle Sum and Difference Identities
These are crucial for simplifying expressions involving the sum or difference of angles:
- sin(A + B) = sin A cos B + cos A sin B
- sin(A - B) = sin A cos B - cos A sin B
- cos(A + B) = cos A cos B - sin A sin B
- cos(A - B) = cos A cos B + sin A sin B
- tan(A + B) = (tan A + tan B) / (1 - tan A tan B)
- tan(A - B) = (tan A - tan B) / (1 + tan A tan B)
Double Angle Identities
These identities express trigonometric functions of 2θ in terms of trigonometric functions of θ:
- sin 2θ = 2 sin θ cos θ
- cos 2θ = cos²θ - sin²θ = 1 - 2sin²θ = 2cos²θ - 1
- tan 2θ = 2 tan θ / (1 - tan²θ)
Half Angle Identities
These identities express trigonometric functions of θ/2 in terms of trigonometric functions of θ:
- sin (θ/2) = ±√[(1 - cos θ) / 2]
- cos (θ/2) = ±√[(1 + cos θ) / 2]
- tan (θ/2) = ±√[(1 - cos θ) / (1 + cos θ)] = sin θ / (1 + cos θ) = (1 - cos θ) / sin θ (Note: the ± depends on the quadrant of θ/2)
Applying the Rules: Solving Trigonometric Problems
The rules and identities outlined above are not just theoretical constructs; they are powerful tools for solving a wide range of problems. Let's explore some examples.
Solving Right-Angled Triangles
Given two sides or one side and one angle (excluding the right angle), we can use sine, cosine, and tangent to find the remaining sides and angles. This is fundamental in surveying, navigation, and engineering.
Solving Non-Right-Angled Triangles
For non-right-angled triangles, we employ the sine rule and the cosine rule:
-
Sine Rule: a/sin A = b/sin B = c/sin C (where a, b, c are the side lengths and A, B, C are the opposite angles)
-
Cosine Rule: a² = b² + c² - 2bc cos A (and similar variations for b² and c²)
Simplifying Trigonometric Expressions
Trigonometric identities are essential for simplifying complex expressions, often encountered in calculus and other advanced mathematical fields. By applying appropriate identities, we can reduce expressions to simpler, more manageable forms.
Modeling Periodic Phenomena
Sine and cosine functions are crucial for modeling periodic phenomena, such as sound waves, light waves, and alternating current. Their properties allow us to describe the oscillatory nature of these phenomena mathematically.
Beyond the Basics: Advanced Trigonometric Concepts
The foundation established so far allows us to delve into more advanced concepts:
-
Inverse Trigonometric Functions: These functions (arcsin, arccos, arctan) find the angle given the value of the trigonometric function.
-
Trigonometric Equations: Solving equations involving trigonometric functions often requires employing identities and algebraic manipulation.
-
Trigonometric Graphs: Visualizing trigonometric functions through their graphs provides valuable insight into their periodic behavior and properties.
-
Complex Numbers and Trigonometry: Trigonometry plays a vital role in representing complex numbers and performing operations with them.
Practical Applications: Where Trigonometry Makes a Difference
Trigonometry's impact extends far beyond the theoretical realm. Its applications are widespread and crucial across diverse fields:
-
Engineering: Calculating forces, stresses, and strains in structures, designing mechanisms, and surveying land.
-
Physics: Analyzing projectile motion, wave phenomena, and oscillations.
-
Computer Graphics: Creating realistic images and animations by manipulating objects in three-dimensional space.
-
Navigation: Determining distances, bearings, and positions using triangulation techniques.
-
Astronomy: Calculating distances to celestial bodies and predicting their movements.
-
Music: Understanding the mathematical relationships between musical notes and intervals.
Conclusion: Mastering the Power of Sin, Cos, and Tan
Sine, cosine, and tangent are fundamental building blocks of trigonometry, a field with far-reaching applications in science, engineering, and beyond. By understanding their definitions, mastering key identities, and practicing their application, you unlock a powerful toolset for solving problems and modelling real-world phenomena. The journey into trigonometry starts with these basic functions, but the depth and breadth of their applications are truly vast and continuously expanding. Continue to explore and experiment, and you will discover the enduring power and elegance of these remarkable mathematical concepts.
Latest Posts
Latest Posts
-
What Is 1 4 1 4 1 4
Apr 06, 2025
-
100 Cm Is Equal To How Many M
Apr 06, 2025
-
How Many Lines Of Symmetry On A Hexagon
Apr 06, 2025
-
Find The Lcm Of 15 And 18
Apr 06, 2025
-
What Is 8 Multiplied By 8
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about Sin And Cos And Tan Rules . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
