Solve For B In Y Mx B
News Co
Apr 19, 2025 · 5 min read
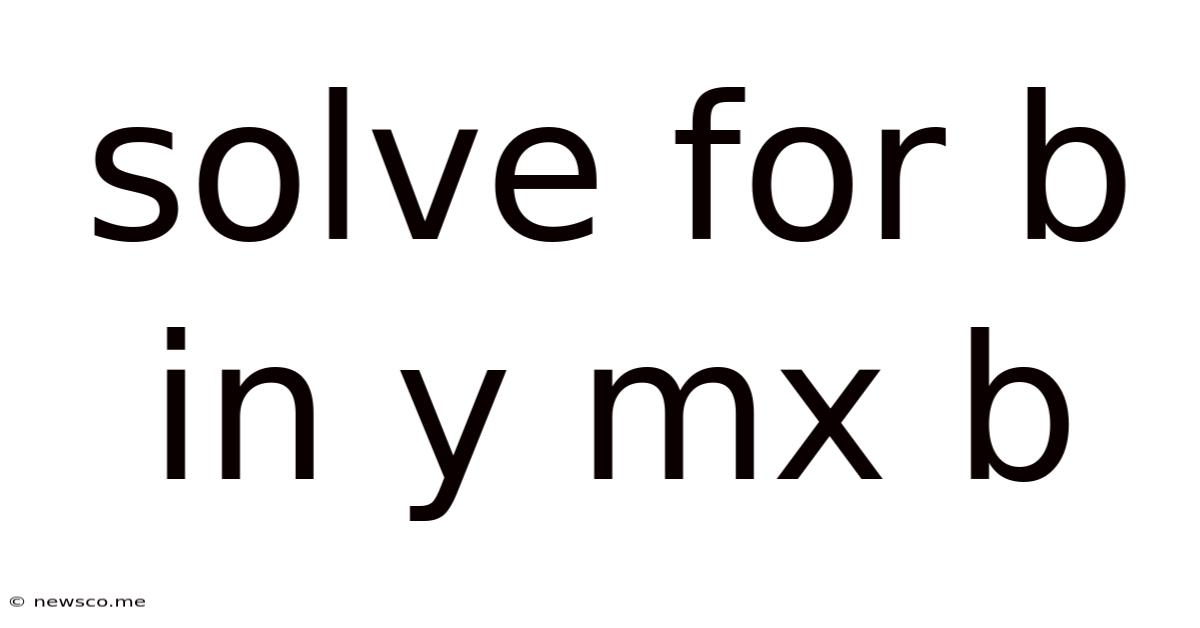
Table of Contents
Solving for 'b' in y = mx + b: A Comprehensive Guide
The equation y = mx + b represents a linear equation in slope-intercept form. Understanding this equation and how to manipulate it is fundamental to algebra and numerous applications in various fields. This comprehensive guide will delve into solving for 'b' in y = mx + b, exploring different scenarios, providing step-by-step solutions, and offering practical examples. We'll also discuss the significance of 'b' and its real-world implications.
Understanding the Components of y = mx + b
Before we jump into solving for 'b', let's refresh our understanding of the components within the equation:
-
y: Represents the dependent variable. Its value depends on the value of x. On a graph, y represents the vertical coordinate.
-
m: Represents the slope of the line. The slope describes the steepness and direction of the line. A positive slope indicates an upward trend, while a negative slope indicates a downward trend. It's calculated as the change in y divided by the change in x (rise over run).
-
x: Represents the independent variable. Its value is independent and can be chosen freely. On a graph, x represents the horizontal coordinate.
-
b: Represents the y-intercept. This is the point where the line crosses the y-axis (where x = 0). It indicates the value of y when x is zero.
Solving for 'b': The Fundamental Approach
Solving for 'b' in y = mx + b is a straightforward algebraic manipulation. The goal is to isolate 'b' on one side of the equation. This is achieved by subtracting 'mx' from both sides:
y = mx + b
y - mx = mx + b - mx
y - mx = b
Therefore, the solution is:
b = y - mx
This simple equation allows us to calculate the y-intercept ('b') if we know the values of y, m, and x.
Practical Applications and Examples
Let's solidify our understanding with some practical examples:
Example 1:
Find the y-intercept ('b') of a line with a slope (m) of 2, passing through the point (3, 8).
-
Given: m = 2, x = 3, y = 8
-
Solution: Using the formula b = y - mx, we substitute the given values:
b = 8 - (2 * 3) = 8 - 6 = 2
-
Therefore, the y-intercept (b) is 2.
Example 2:
A line has a slope of -1/2 and passes through the point (-4, 5). What is the y-intercept?
-
Given: m = -1/2, x = -4, y = 5
-
Solution: Substituting into the formula:
b = 5 - (-1/2 * -4) = 5 - 2 = 3
-
Therefore, the y-intercept (b) is 3.
Example 3: Real-world Application - Calculating Profit
Imagine a small business selling handmade candles. Their profit (y) is determined by the number of candles sold (x) and their profit margin (m). The fixed costs (rent, utilities, etc.) represent the y-intercept (b). If they sold 100 candles (x = 100), made a profit of $500 (y = 500), and their profit margin per candle is $4 (m = 4), we can calculate their fixed costs:
-
Given: m = 4, x = 100, y = 500
-
Solution:
b = 500 - (4 * 100) = 500 - 400 = 100
-
Therefore, their fixed costs (y-intercept) are $100.
Solving for 'b' When Given Two Points
If you're not given the slope (m), but instead two points on the line, you'll need to first calculate the slope before solving for 'b'.
Steps:
-
Calculate the slope (m): Use the formula m = (y₂ - y₁) / (x₂ - x₁), where (x₁, y₁) and (x₂, y₂) are the coordinates of the two points.
-
Choose one point: Select either of the two points.
-
Substitute values: Substitute the calculated slope (m) and the chosen point's coordinates (x, y) into the formula b = y - mx.
-
Solve for b: Perform the calculation to find the y-intercept.
Example 4:
Find the y-intercept of a line passing through points (1, 3) and (4, 9).
-
Calculate the slope: m = (9 - 3) / (4 - 1) = 6 / 3 = 2
-
Choose a point: Let's use (1, 3).
-
Substitute values: b = 3 - (2 * 1) = 3 - 2 = 1
-
Therefore, the y-intercept (b) is 1.
The Significance of the y-intercept ('b')
The y-intercept holds significant meaning in various contexts. It represents the starting point or initial value of the dependent variable when the independent variable is zero.
-
In linear graphs: It's the point where the line intersects the y-axis.
-
In business: It often represents fixed costs, initial investment, or starting inventory.
-
In science: It might represent the initial amount of a substance, the baseline measurement, or the starting point of a process.
-
In programming: It can represent an initial value or a default setting.
Advanced Scenarios and Considerations
While the basic approach remains consistent, certain scenarios might require extra steps:
-
Parallel lines: If two lines are parallel, they share the same slope (m). Knowing this and a point on one of the lines allows you to calculate its y-intercept.
-
Perpendicular lines: The slopes of perpendicular lines are negative reciprocals of each other. This information, combined with a point on one of the lines, can help determine the y-intercept of the other line.
-
Systems of equations: Solving for 'b' might be part of a larger system of equations, requiring simultaneous equation solving techniques to find the value of 'b'.
Conclusion: Mastering the Power of y = mx + b
Solving for 'b' in y = mx + b is a fundamental skill in algebra with widespread applications. Understanding this process not only allows you to determine the y-intercept but also enhances your comprehension of linear equations, their graphical representations, and their practical uses across various disciplines. By mastering this simple yet powerful algebraic manipulation, you equip yourself with a valuable tool for solving real-world problems and analyzing data effectively. Remember to practice regularly with different examples to solidify your understanding and build confidence in your algebraic abilities. The more you practice, the more intuitive this process will become.
Latest Posts
Related Post
Thank you for visiting our website which covers about Solve For B In Y Mx B . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.