Solve For X 5 X 10 30 15x
News Co
Apr 14, 2025 · 4 min read
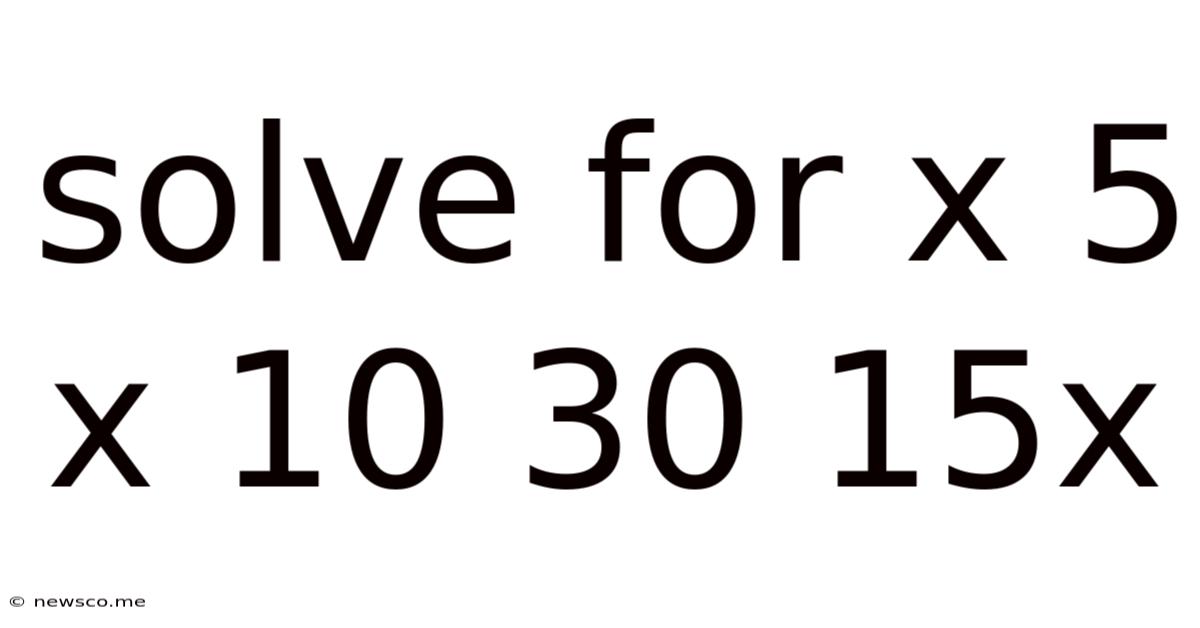
Table of Contents
Solving for x: A Comprehensive Guide to Algebraic Equations
This article delves into the process of solving for 'x' in the equation 5x + 10 = 30 + 15x, providing a step-by-step explanation suitable for beginners and a deeper exploration for more advanced learners. We'll cover various approaches, emphasizing understanding the underlying principles of algebra.
Understanding the Equation
Before we begin solving, let's break down the equation 5x + 10 = 30 + 15x. This is a linear equation, meaning the highest power of 'x' is 1. It involves:
- Variables: 'x' is the variable, an unknown value we need to find.
- Constants: 10 and 30 are constants, fixed numerical values.
- Coefficients: 5 and 15 are coefficients, numbers multiplying the variable 'x'.
- Equality: The '=' sign indicates that both sides of the equation have the same value.
Our goal is to isolate 'x' on one side of the equation to find its value.
Solving for x: A Step-by-Step Approach
There are several ways to approach this problem. Let's use a systematic approach focusing on maintaining the equality of both sides:
Step 1: Combine Like Terms
Our equation is 5x + 10 = 30 + 15x. Notice we have 'x' terms on both sides. To simplify, let's move all the 'x' terms to one side and the constants to the other. We can achieve this by subtracting 5x from both sides:
5x + 10 - 5x = 30 + 15x - 5x
This simplifies to:
10 = 30 + 10x
Next, subtract 30 from both sides to isolate the 'x' term:
10 - 30 = 30 + 10x - 30
This simplifies to:
-20 = 10x
Step 2: Isolate x
Now we have -20 = 10x. To isolate 'x', we need to divide both sides by 10 (the coefficient of 'x'):
-20 / 10 = 10x / 10
This gives us:
-2 = x
Therefore, the solution to the equation is x = -2.
Verification: Checking Your Solution
It's crucial to verify your solution by substituting the value of 'x' back into the original equation:
5x + 10 = 30 + 15x
Substitute x = -2:
5(-2) + 10 = 30 + 15(-2)
-10 + 10 = 30 - 30
0 = 0
Since both sides are equal, our solution x = -2 is correct.
Alternative Methods: Rearranging the Equation
While the previous method is straightforward, let's explore alternative approaches to solving for 'x':
Method 1: Subtracting Constants First
Instead of moving the 'x' terms first, we can start by subtracting 10 from both sides:
5x + 10 - 10 = 30 + 15x - 10
This simplifies to:
5x = 20 + 15x
Now, subtract 15x from both sides:
5x - 15x = 20 + 15x - 15x
-10x = 20
Divide both sides by -10:
-10x / -10 = 20 / -10
x = -2
This yields the same result, demonstrating the flexibility in solving linear equations.
Method 2: Using the Distributive Property (for more complex equations)
While not necessary for this specific equation, the distributive property becomes crucial when dealing with more complex equations involving parentheses. The distributive property states that a(b + c) = ab + ac. Let's consider a hypothetical example:
2(x + 3) = 10
Applying the distributive property:
2x + 6 = 10
Subtracting 6 from both sides:
2x = 4
Dividing by 2:
x = 2
Solving Linear Equations: General Principles
The principles demonstrated above are applicable to solving a wide range of linear equations. Key takeaways include:
- Maintain Equality: Any operation performed on one side of the equation must be performed on the other to maintain balance.
- Combine Like Terms: Simplify the equation by grouping similar terms (variables and constants).
- Isolate the Variable: Manipulate the equation to have the variable ('x' in our case) on one side and the constant on the other.
- Verify Your Solution: Always check your answer by substituting it back into the original equation.
Troubleshooting Common Mistakes
Beginners often encounter some common errors when solving linear equations. Let's address these:
- Incorrect Sign Changes: Remember that when moving terms across the equal sign, the sign changes. For example, +5x becomes -5x when moved to the other side.
- Errors in Arithmetic: Double-check your calculations throughout the process to avoid arithmetic mistakes.
- Forgetting to Distribute: When dealing with parentheses, remember to distribute correctly before proceeding with other steps.
Advanced Applications and Extensions
The ability to solve linear equations is fundamental in various mathematical fields, including:
- Calculus: Solving for variables is crucial in finding derivatives and integrals.
- Physics and Engineering: Linear equations are essential for modeling and solving numerous physical problems.
- Computer Science: Solving equations is vital in algorithm design and data analysis.
Conclusion: Mastering the Fundamentals
Solving for 'x' in an equation like 5x + 10 = 30 + 15x isn't merely an algebraic exercise; it's a foundational skill that underpins numerous mathematical and scientific disciplines. By understanding the principles of maintaining equality, combining like terms, and isolating the variable, you can confidently tackle more complex equations and unlock a deeper appreciation for the power of algebra. Remember to practice regularly and check your work to solidify your understanding and avoid common mistakes. Consistent practice will build your confidence and proficiency in solving linear equations and beyond.
Latest Posts
Related Post
Thank you for visiting our website which covers about Solve For X 5 X 10 30 15x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.