Solve The Compound Inequality 6b 24 Or 4b 12 4
News Co
Mar 26, 2025 · 5 min read
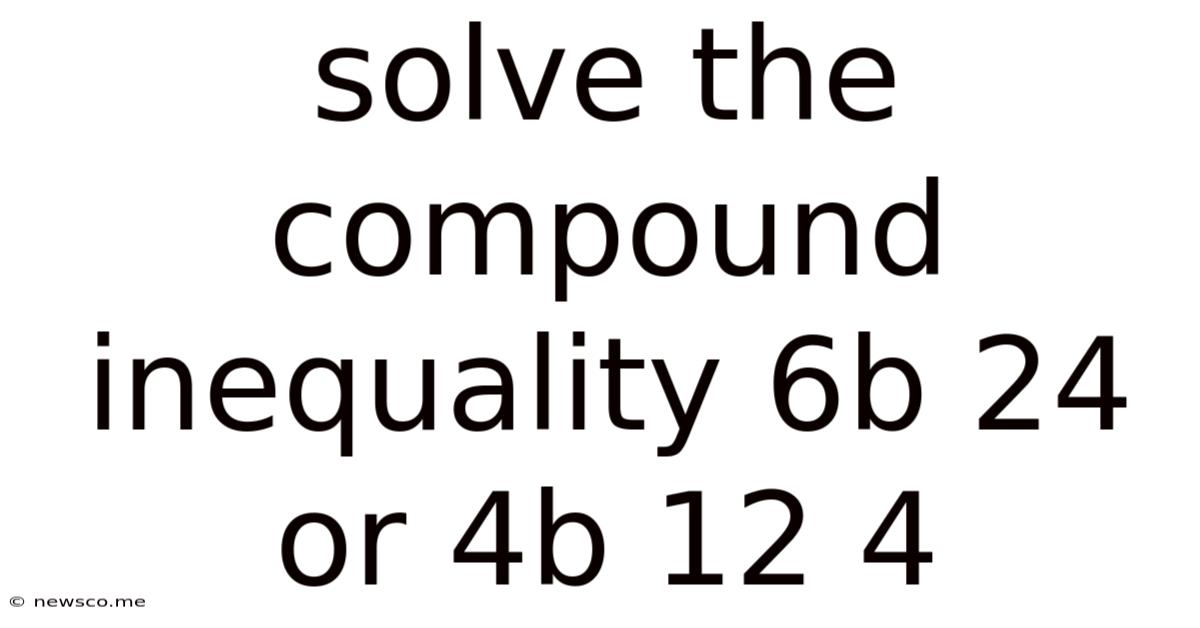
Table of Contents
Solving Compound Inequalities: A Comprehensive Guide
Compound inequalities involve two or more inequalities joined by the words "and" or "or." Solving them requires understanding the individual inequalities and how the connecting word affects the solution set. This article will delve into the process of solving compound inequalities, focusing specifically on the example: 6b > 24 or 4b + 12 < 4. We'll explore the steps involved, common pitfalls to avoid, and how to represent the solution graphically and using interval notation.
Understanding the Problem: 6b > 24 or 4b + 12 < 4
Our compound inequality consists of two separate inequalities:
- 6b > 24
- 4b + 12 < 4
The word "or" connects these inequalities. This means that a solution satisfies the compound inequality if it satisfies at least one of the individual inequalities. This is different from inequalities connected by "and," where a solution must satisfy both inequalities simultaneously.
Solving the First Inequality: 6b > 24
Let's solve the first inequality, 6b > 24, step-by-step:
-
Isolate the variable: To isolate 'b', we divide both sides of the inequality by 6. Remember, when dividing or multiplying an inequality by a negative number, you must reverse the inequality sign. In this case, we're dividing by a positive number, so the inequality sign remains the same.
6b / 6 > 24 / 6
-
Simplify: This simplifies to:
b > 4
This means that any value of 'b' greater than 4 satisfies this inequality.
Solving the Second Inequality: 4b + 12 < 4
Now let's tackle the second inequality, 4b + 12 < 4:
-
Subtract 12 from both sides: This step aims to isolate the term with 'b'.
4b + 12 - 12 < 4 - 12
-
Simplify: This gives us:
4b < -8
-
Divide both sides by 4: Again, we're dividing by a positive number, so the inequality sign remains unchanged.
4b / 4 < -8 / 4
-
Simplify: This results in:
b < -2
This inequality means that any value of 'b' less than -2 satisfies this inequality.
Combining the Solutions: The "or" Condition
Because our compound inequality uses "or," we need to consider the union of the solution sets from both individual inequalities. This means we take all the values that satisfy either b > 4 or b < -2.
Representing the Solution: Graphically and in Interval Notation
Graphical Representation
The solution can be represented graphically on a number line. We'll have two separate regions:
- b > 4: This is represented by an open circle at 4 (because 4 is not included in the solution) and an arrow extending to the right, indicating all values greater than 4.
- b < -2: This is represented by an open circle at -2 (again, -2 is not included) and an arrow extending to the left, indicating all values less than -2.
[Insert a number line graph here showing open circles at -2 and 4, with arrows extending to the left from -2 and to the right from 4.]
Interval Notation
In interval notation, the solution is expressed as:
(-∞, -2) ∪ (4, ∞)
- (-∞, -2): This represents all real numbers less than -2. The parenthesis indicates that -2 is not included.
- (4, ∞): This represents all real numbers greater than 4. Again, the parenthesis signifies that 4 is not included.
- ∪: This symbol represents the union of the two intervals, meaning we combine both sets of solutions.
Further Exploration: Compound Inequalities with "and"
Let's briefly contrast this with a compound inequality using "and." Suppose we had:
6b > 24 and 4b + 12 < 4
In this scenario, a value of 'b' must satisfy both inequalities simultaneously. Since we already know the solutions for each inequality (b > 4 and b < -2), we look for the overlap. There is no overlap; no single value can be simultaneously greater than 4 and less than -2. Therefore, the solution to this "and" compound inequality is the empty set, often represented as {} or Ø. Graphically, this would be represented by an empty number line. In interval notation, there is no interval to represent.
Common Mistakes to Avoid when Solving Compound Inequalities
- Ignoring the connecting word: Carefully note whether the inequalities are connected by "and" or "or." This determines how you combine the solution sets.
- Incorrectly reversing the inequality sign: Remember to reverse the inequality sign only when multiplying or dividing by a negative number.
- Incorrectly graphing the solution: Pay close attention to whether the endpoints are included (closed circles) or excluded (open circles) on the number line graph.
- Errors in simplifying expressions: Double-check your algebra to avoid errors in simplifying expressions, which can lead to incorrect solutions.
Advanced Applications of Compound Inequalities
Compound inequalities find applications in various fields:
- Engineering: Designing systems with constraints on multiple parameters.
- Finance: Modeling investment strategies with risk and return limitations.
- Computer Science: Defining ranges for data types and variables.
- Statistics: Establishing confidence intervals and determining significant values.
Understanding compound inequalities is crucial for success in many quantitative fields.
Conclusion: Mastering Compound Inequalities
Solving compound inequalities, whether connected by "or" or "and," requires careful attention to detail and a solid grasp of basic inequality principles. By following the steps outlined above and avoiding common errors, you can confidently solve even complex compound inequalities, represent the solution graphically and in interval notation, and apply this knowledge to solve real-world problems. Consistent practice and understanding of the "or" and "and" conditions are key to mastering this fundamental mathematical concept. Remember to always check your work to ensure your solutions are accurate and reflect the true nature of the inequality problem presented.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about Solve The Compound Inequality 6b 24 Or 4b 12 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.