Solve The Equation 3x 1 10x X 4
News Co
Apr 22, 2025 · 5 min read
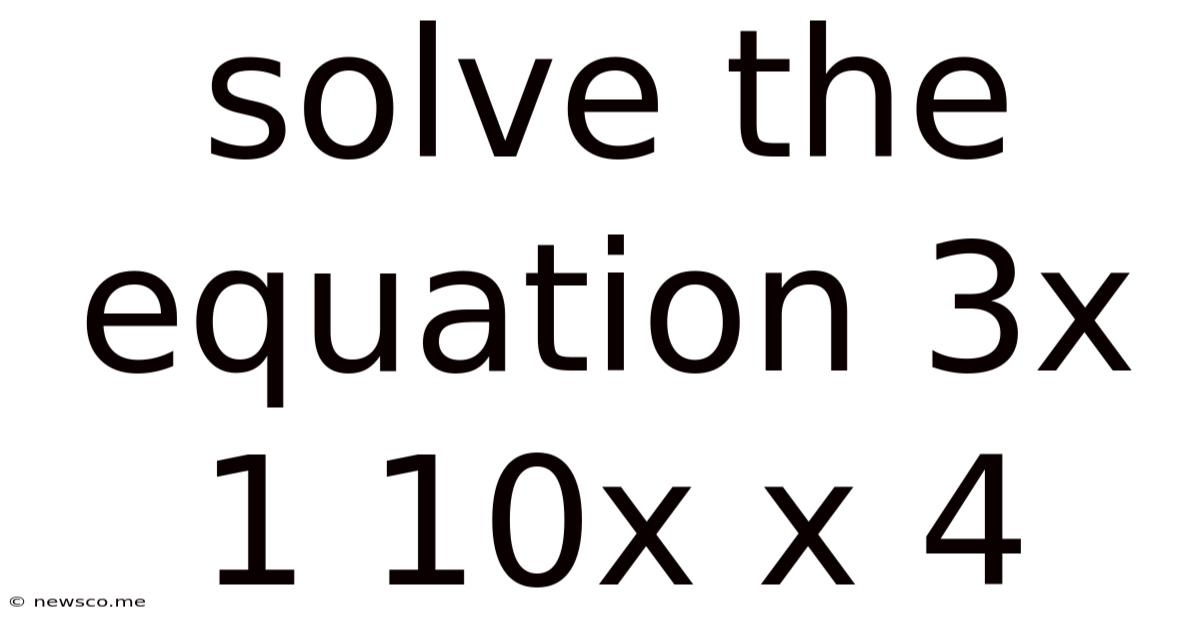
Table of Contents
Solving the Equation: 3x + 1 = 10x - x + 4
This article provides a comprehensive guide to solving the algebraic equation 3x + 1 = 10x - x + 4. We'll break down the process step-by-step, explaining the underlying principles of algebra involved, and offering tips and tricks for similar equation-solving problems. This detailed walkthrough will be beneficial for students learning algebra and anyone looking to refresh their math skills. We'll also explore the concept of verifying solutions and discuss potential real-world applications of such equations.
Understanding the Equation
Before we begin solving, let's understand the structure of the equation: 3x + 1 = 10x - x + 4. This is a linear equation because the highest power of the variable 'x' is 1. The goal is to find the value of 'x' that makes the equation true—that is, the value that makes the left-hand side (LHS) equal to the right-hand side (RHS).
The equation contains:
- Variables: 'x' represents an unknown quantity.
- Constants: 1 and 4 are constant numerical values.
- Coefficients: 3, 10, and -1 are the numerical factors multiplying the variable 'x'.
Step-by-Step Solution
The key to solving linear equations is to isolate the variable 'x' on one side of the equation. We achieve this through a series of algebraic manipulations, ensuring that we maintain the equality of both sides at each step.
Step 1: Simplify the Right-Hand Side (RHS)
Notice that on the RHS, we have two terms containing 'x': 10x and -x. We can combine these like terms:
10x - x = 9x
The equation now becomes:
3x + 1 = 9x + 4
Step 2: Move the Variable Terms to One Side
To isolate 'x', let's move all the terms containing 'x' to one side of the equation and the constant terms to the other side. We can subtract 3x from both sides:
3x + 1 - 3x = 9x + 4 - 3x
This simplifies to:
1 = 6x + 4
Step 3: Move the Constant Terms to the Other Side
Next, let's isolate the term with 'x' by subtracting 4 from both sides:
1 - 4 = 6x + 4 - 4
This simplifies to:
-3 = 6x
Step 4: Solve for x
Finally, to find the value of 'x', we divide both sides by the coefficient of 'x', which is 6:
-3 / 6 = 6x / 6
This gives us:
x = -1/2 or x = -0.5
Therefore, the solution to the equation 3x + 1 = 10x - x + 4 is x = -1/2 or x = -0.5.
Verifying the Solution
It's always a good practice to verify the solution by substituting the value of 'x' back into the original equation. Let's check if x = -1/2 is correct:
LHS: 3(-1/2) + 1 = -3/2 + 1 = -1/2
RHS: 10(-1/2) - (-1/2) + 4 = -5 + 1/2 + 4 = -1/2
Since LHS = RHS, our solution x = -1/2 is correct.
Alternative Methods for Solving Linear Equations
While the step-by-step method is generally preferred for its clarity, other approaches can be used to solve linear equations. These include:
-
Using a graphical method: Plotting both sides of the equation as separate lines on a graph. The x-coordinate of the point where the lines intersect represents the solution.
-
Using matrices (for systems of linear equations): While not directly applicable to a single linear equation like this one, matrix methods are highly useful for solving systems of multiple linear equations simultaneously.
Applications of Linear Equations
Linear equations like this one are fundamental to many areas of mathematics and science. Here are a few examples of their real-world applications:
-
Physics: Describing the motion of objects (e.g., calculating velocity or acceleration).
-
Engineering: Modeling relationships between different variables in engineering systems (e.g., stress-strain relationships in materials).
-
Economics: Representing economic models and relationships (e.g., supply and demand curves).
-
Finance: Calculating interest earned or owed, predicting future financial values.
-
Computer Science: Algorithm analysis and optimization.
Troubleshooting Common Errors
When solving linear equations, several common mistakes can occur. Here are some points to be mindful of:
-
Incorrectly combining like terms: Make sure you are only adding or subtracting terms that have the same variable raised to the same power.
-
Errors in arithmetic: Carefully check your addition, subtraction, multiplication, and division operations.
-
Incorrectly applying the order of operations (PEMDAS/BODMAS): Remember the order of operations: Parentheses/Brackets, Exponents/Orders, Multiplication and Division (from left to right), Addition and Subtraction (from left to right).
-
Losing track of negative signs: Be extra cautious with negative numbers; a misplaced negative sign can completely change the outcome.
Expanding on the Concept: Systems of Linear Equations
While this article focused on solving a single linear equation, many real-world problems involve multiple linear equations. These are known as systems of linear equations. Solving systems of linear equations can be achieved through various methods, including:
-
Substitution method: Solving one equation for one variable and substituting that expression into the other equation.
-
Elimination method: Multiplying equations by constants to eliminate a variable when adding or subtracting the equations.
-
Graphical method: Plotting the equations on a graph; the point of intersection represents the solution.
-
Matrix methods: Using matrices and Gaussian elimination or other matrix operations to solve the system.
Conclusion: Mastering Linear Equations
Solving linear equations is a fundamental skill in algebra and has widespread applications across various disciplines. By understanding the underlying principles and practicing regularly, you can confidently tackle more complex algebraic problems. Remember to carefully follow the step-by-step process, verify your solutions, and be aware of common pitfalls. With consistent practice, you'll master the art of solving linear equations and unlock their power in various real-world applications. Further exploration into systems of linear equations will expand your problem-solving capabilities even more. This detailed explanation of solving 3x + 1 = 10x - x + 4 not only provides a solution but also equips you with the knowledge and tools necessary to tackle similar algebraic challenges with confidence.
Latest Posts
Related Post
Thank you for visiting our website which covers about Solve The Equation 3x 1 10x X 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.