Solve The Equation 6 2x 4 2 2x 4 2
News Co
Mar 15, 2025 · 4 min read
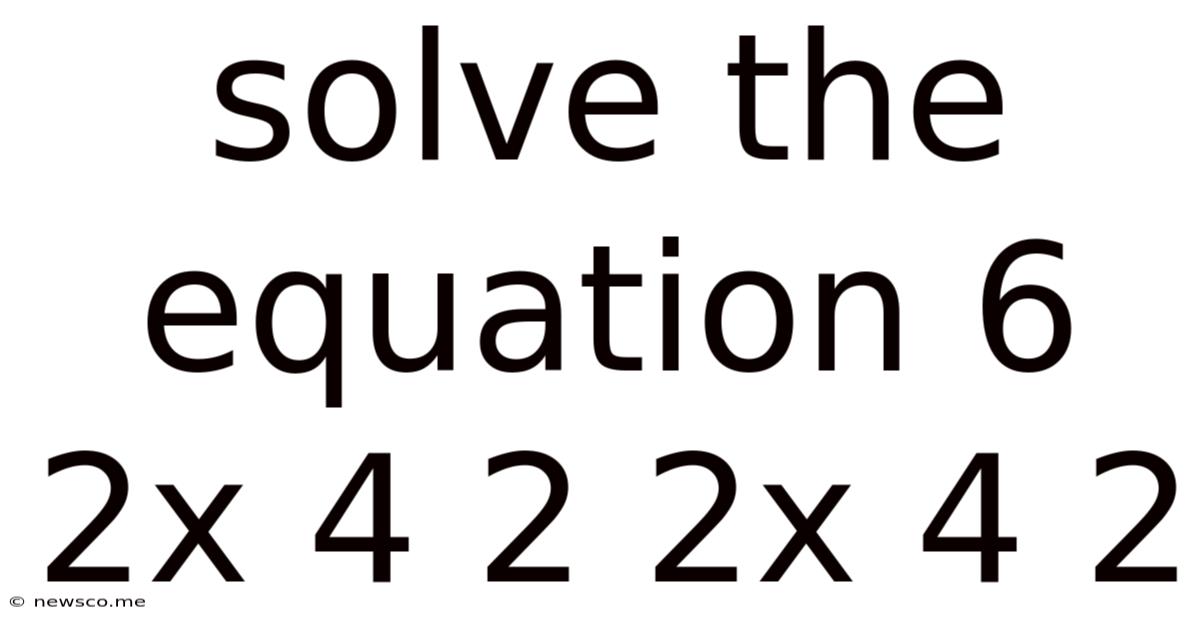
Table of Contents
Solving the Equation: 6^(2x) + 4^(2x) = 2^(2x) + 4
This article delves into the process of solving the equation 6^(2x) + 4^(2x) = 2^(2x) + 4. We'll explore various mathematical techniques, including algebraic manipulation, logarithmic properties, and numerical methods, to find the solution(s) for 'x'. We will also discuss the importance of verifying solutions and the potential pitfalls of certain approaches. This comprehensive guide aims to provide a clear and detailed understanding of the problem-solving process.
Understanding the Equation
The equation we're tackling, 6^(2x) + 4^(2x) = 2^(2x) + 4, is a transcendental equation because the variable 'x' is part of an exponent. This type of equation often requires more sophisticated techniques than simple linear or quadratic equations. Notice the presence of multiple exponential terms with different bases (6, 4, and 2). This adds complexity to the solution process.
Attempting Algebraic Manipulation
Our first approach involves attempting to manipulate the equation algebraically. We can rewrite the equation using the properties of exponents:
(6^2)^x + (4^2)^x = 2^(2x) + 4
This simplifies to:
36^x + 16^x = 2^(2x) + 4
Unfortunately, directly manipulating this equation to isolate 'x' proves challenging. The different bases prevent simple factorization or substitution. We can't easily combine the exponential terms due to their varying bases. This leads us to explore alternative methods.
Introducing Logarithms
A common technique for solving exponential equations is to use logarithms. Taking the logarithm of both sides can help simplify the equation, particularly if we can apply logarithm properties to separate the variable 'x'. Let's try using the natural logarithm (ln):
ln(36^x + 16^x) = ln(2^(2x) + 4)
However, the presence of the sums within the logarithms prevents us from easily applying the logarithm power rule (ln(a^b) = b * ln(a)). The logarithm of a sum is not equal to the sum of logarithms (ln(a + b) ≠ ln(a) + ln(b)). This inherent property of logarithms hinders our ability to directly solve using this approach.
Numerical Methods: An Iterative Approach
Since algebraic and logarithmic manipulations prove ineffective, we can turn to numerical methods. These methods involve iterative approximation to find a solution. One common numerical method is the Newton-Raphson method. However, applying the Newton-Raphson method to this equation requires calculating the derivative of a complex function, which can be cumbersome. Other iterative methods like the bisection method or fixed-point iteration might be more suitable, but they require careful selection of initial guesses and can be computationally intensive.
Graphical Representation and Solution Estimation
A graphical approach can provide valuable insight. We can plot the two functions:
y = 36^x + 16^x
and
y = 2^(2x) + 4
The intersection point(s) of these two curves represent the solution(s) to the equation. Using graphing software or a calculator, we can visually estimate the value of 'x' where the curves intersect. This graphical method provides a quick way to get an approximate solution, but it won't yield a precise analytical solution.
Refining the Numerical Approach: Bisection Method
Let's illustrate the bisection method, a relatively simple numerical technique. We need to find an interval [a, b] where the function f(x) = 36^x + 16^x - 2^(2x) - 4 changes sign. This indicates that a root lies within the interval.
Let's test some values:
- f(0) = 1 + 1 - 1 - 4 = -3
- f(1) = 36 + 16 - 4 - 4 = 44
- f(0.5) ≈ 6.7 + 4.0 - 2.828 - 4 ≈ 3.872
Since f(0) < 0 and f(0.5) > 0, there's a root between 0 and 0.5. The bisection method repeatedly halves the interval, checking for sign changes, until the root is approximated to a desired level of accuracy.
This iterative process continues, narrowing down the interval until we reach a satisfactory approximation of the solution. The more iterations we perform, the greater the accuracy of the approximate solution.
Importance of Verification
Regardless of the method used – graphical estimation, numerical methods, or any other technique – it's crucial to verify the solution(s). Substitute the obtained value(s) of 'x' back into the original equation to check if they satisfy the equality. This verification step is essential to ensure the accuracy of the result and eliminate any potential errors during the solution process.
Challenges and Considerations
Solving this equation highlights the complexities involved in handling transcendental equations. The lack of a straightforward algebraic solution necessitates the use of numerical methods, which involve approximation and iterative calculations. The accuracy of the solution depends on the method used and the number of iterations performed. Different numerical methods have varying convergence rates and computational complexities.
Conclusion: A Multifaceted Problem
The equation 6^(2x) + 4^(2x) = 2^(2x) + 4 presents a compelling challenge, requiring a combination of mathematical techniques and a deep understanding of their limitations. While a closed-form, analytical solution remains elusive, we've explored multiple approaches, including algebraic manipulation, logarithmic considerations, and numerical methods like the bisection method. The graphical approach provides a useful visual aid for estimating solutions, while numerical methods provide a path towards obtaining approximate solutions with desired accuracy. The key takeaway is the importance of understanding the strengths and weaknesses of different mathematical techniques and employing appropriate strategies based on the characteristics of the problem at hand. The verification step, often overlooked, remains critical to ensure the validity of any obtained solution.
Latest Posts
Related Post
Thank you for visiting our website which covers about Solve The Equation 6 2x 4 2 2x 4 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.