Solve The Equation X 8 3x X 6
News Co
Mar 17, 2025 · 4 min read
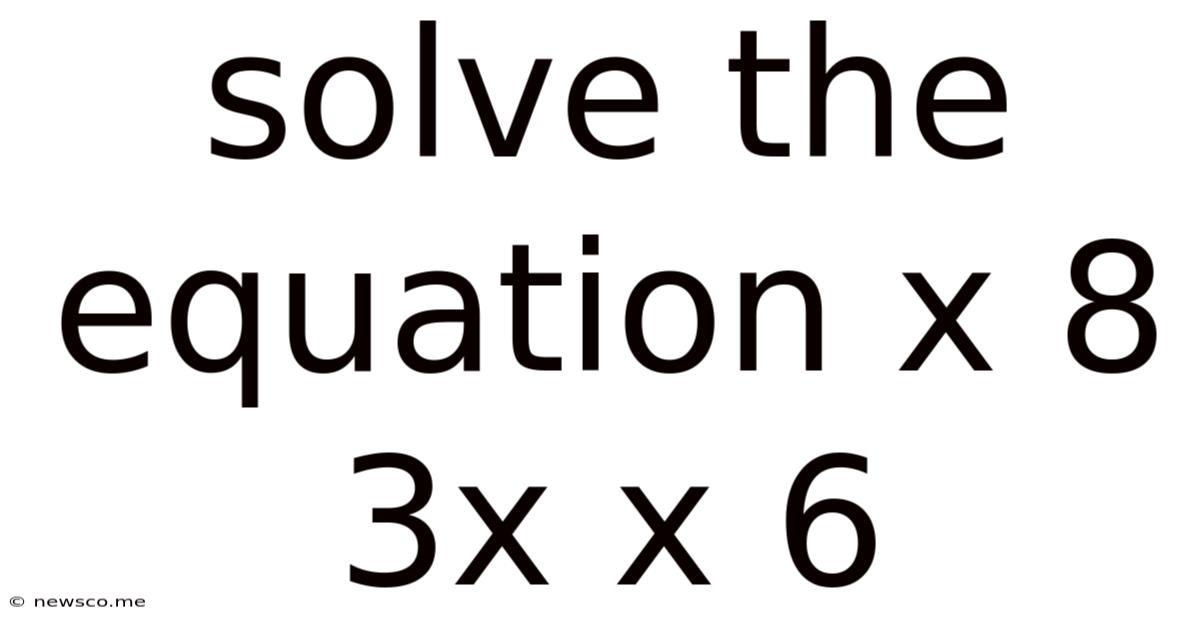
Table of Contents
Solving the Equation x⁸ + 3x = x⁶ + 6
This article delves into the intricacies of solving the polynomial equation x⁸ + 3x = x⁶ + 6. We'll explore various methods, from basic algebraic manipulation to more advanced techniques, ultimately aiming to find all real and complex solutions. Understanding this equation requires a solid grasp of polynomial equations, factoring, and numerical methods. Let's embark on this mathematical journey!
Understanding the Equation
The given equation, x⁸ + 3x = x⁶ + 6, is a polynomial equation of degree 8. This means it can have up to eight solutions (roots). These solutions can be real numbers or complex numbers (numbers involving the imaginary unit 'i', where i² = -1). Our goal is to find all these solutions.
The first step in solving any polynomial equation is to rearrange it into standard form, where one side equals zero:
x⁸ - x⁶ + 3x - 6 = 0
This form makes it easier to apply various solving techniques.
Attempting Factoring
Factoring is a crucial technique in solving polynomial equations. It involves expressing the polynomial as a product of simpler polynomials. Unfortunately, directly factoring this eighth-degree polynomial is quite challenging. There's no readily apparent common factor, and the standard factoring methods (e.g., grouping, quadratic formula) don't readily apply.
We can attempt to look for rational roots using the Rational Root Theorem. This theorem states that any rational root of a polynomial with integer coefficients must be of the form p/q, where 'p' is a factor of the constant term and 'q' is a factor of the leading coefficient.
In our equation, the constant term is -6 and the leading coefficient is 1. Therefore, potential rational roots are ±1, ±2, ±3, and ±6. We can test these values by substituting them into the equation:
- x = 1: 1⁸ - 1⁶ + 3(1) - 6 = -3 ≠ 0
- x = -1: (-1)⁸ - (-1)⁶ + 3(-1) - 6 = -9 ≠ 0
- x = 2: 2⁸ - 2⁶ + 3(2) - 6 = 256 - 64 + 6 - 6 = 192 ≠ 0
- x = -2: (-2)⁸ - (-2)⁶ + 3(-2) - 6 = 256 - 64 - 6 - 6 = 180 ≠ 0
- x = 3: 3⁸ - 3⁶ + 3(3) - 6 = 6561 - 729 + 9 - 6 = 5845 ≠ 0
- x = -3: (-3)⁸ - (-3)⁶ + 3(-3) - 6 = 6561 - 729 - 9 - 6 = 5827 ≠ 0
- x = 6: 6⁸ - 6⁶ + 3(6) - 6 = 1679616 - 46656 + 18 - 6 = 1632972 ≠ 0
- x = -6: (-6)⁸ - (-6)⁶ + 3(-6) - 6 = 1679616 - 46656 - 18 - 6 = 1632946 ≠ 0
None of these potential rational roots are actual solutions. This suggests that the equation likely has irrational or complex roots.
Numerical Methods
Since factoring proves difficult, we can turn to numerical methods to approximate the solutions. These methods iteratively refine an initial guess to get closer to the actual root. Some common numerical methods include:
- Newton-Raphson Method: This method uses the derivative of the function to iteratively improve the approximation.
- Bisection Method: This method repeatedly divides an interval containing a root in half until the root is found within a desired tolerance.
- Secant Method: This method uses a secant line to approximate the root.
These methods require an initial guess for the root and typically involve iterative calculations. Software packages like MATLAB, Python (with libraries like SciPy), or online calculators can readily perform these calculations.
Graphical Approach
A graphical approach can provide insights into the approximate locations of the roots. Plotting the function f(x) = x⁸ - x⁶ + 3x - 6 will reveal where the graph intersects the x-axis (where f(x) = 0). Software like Desmos or GeoGebra can be used for this purpose. The graph will show the approximate real roots; however, it won't reveal complex roots directly.
Advanced Techniques
For a definitive solution, more advanced techniques might be necessary. These include:
- Cardano's Method: Useful for solving cubic equations. While not directly applicable to our eighth-degree equation, it could be relevant if the equation could be reduced to a cubic through substitution or transformation.
- Ferrari's Method: A method for solving quartic (fourth-degree) equations. Again, this might be relevant if the equation can be simplified.
- Numerical Root-Finding Algorithms: Sophisticated algorithms implemented in mathematical software packages can handle higher-degree polynomials and provide accurate approximations of all roots, both real and complex.
Conclusion
Solving the equation x⁸ + 3x = x⁶ + 6, or equivalently x⁸ - x⁶ + 3x - 6 = 0, is a challenging problem that likely doesn't have simple, easily factorable solutions. While basic algebraic techniques like factoring and the Rational Root Theorem prove insufficient, numerical methods offer practical ways to approximate the real roots. More advanced methods, often requiring computational assistance, are needed to find all eight roots, including any complex solutions. The graphical approach offers a visual representation and helps estimate the real roots. Understanding the limitations of different methods and appropriately selecting the best technique based on the problem is crucial in solving such polynomial equations. Remember, exploring different approaches often provides a deeper understanding of the equation's nature and its solutions.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about Solve The Equation X 8 3x X 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.