Solve The Inequality 2 4 2x 5x 5
News Co
May 07, 2025 · 4 min read
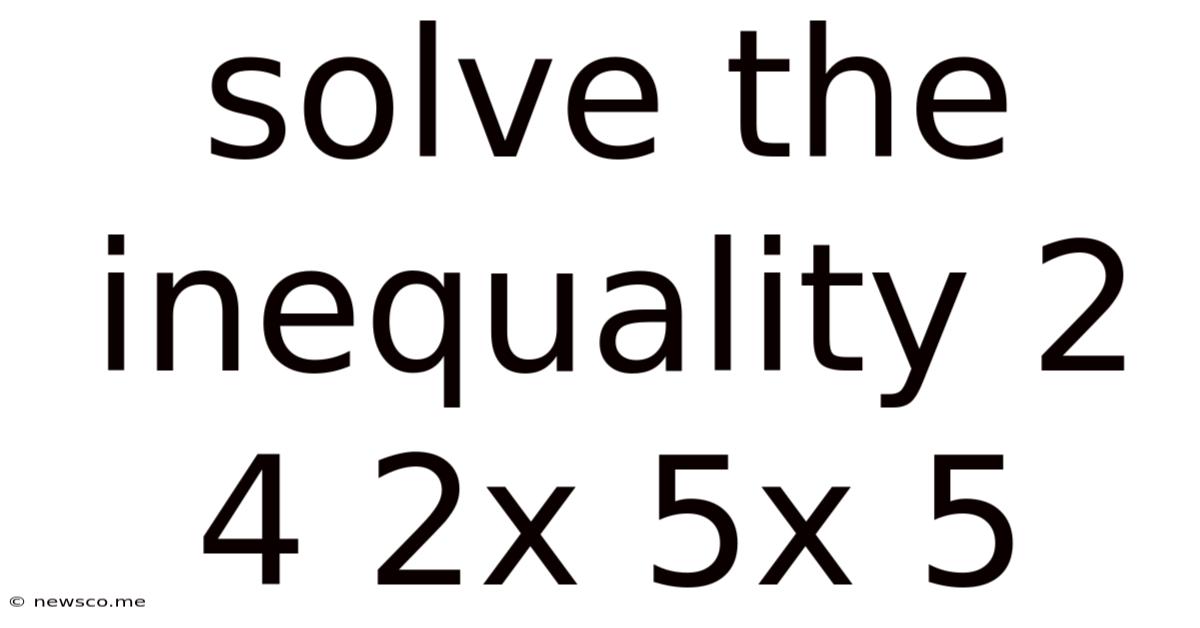
Table of Contents
Solving the Inequality: 2 ≤ 4 - 2x < 5x + 5
This article provides a comprehensive guide on how to solve the compound inequality 2 ≤ 4 - 2x < 5x + 5. We will break down the process step-by-step, explaining the underlying principles and offering helpful tips for similar problems. Understanding how to solve compound inequalities is crucial for various mathematical applications, from calculus to linear programming.
Understanding Compound Inequalities
A compound inequality is an inequality that combines two or more inequalities using the words "and" or "or." In our case, we have a compound inequality involving three expressions: 2, 4 - 2x, and 5x + 5. The inequality states that the expression 4 - 2x is greater than or equal to 2 AND simultaneously less than 5x + 5. This means we must find the range of values for 'x' that satisfy both conditions simultaneously.
Solving the Inequality: A Step-by-Step Approach
To solve the inequality 2 ≤ 4 - 2x < 5x + 5, we need to solve two separate inequalities:
- 2 ≤ 4 - 2x
- 4 - 2x < 5x + 5
Let's tackle each inequality individually:
1. Solving 2 ≤ 4 - 2x
Step 1: Isolate the term with 'x'. Subtract 4 from both sides of the inequality:
2 - 4 ≤ 4 - 2x - 4
This simplifies to:
-2 ≤ -2x
Step 2: Solve for 'x'. Divide both sides by -2. Remember, when dividing or multiplying an inequality by a negative number, you must reverse the inequality sign:
(-2)/(-2) ≥ (-2x)/(-2)
This simplifies to:
1 ≥ x or x ≤ 1
2. Solving 4 - 2x < 5x + 5
Step 1: Isolate the terms with 'x'. Add 2x to both sides:
4 - 2x + 2x < 5x + 5 + 2x
This simplifies to:
4 < 7x + 5
Step 2: Isolate the term with 'x'. Subtract 5 from both sides:
4 - 5 < 7x + 5 - 5
This simplifies to:
-1 < 7x
Step 3: Solve for 'x'. Divide both sides by 7:
(-1)/7 < (7x)/7
This simplifies to:
-1/7 < x or x > -1/7
Combining the Solutions
Now that we've solved both inequalities, we need to find the values of 'x' that satisfy both conditions: x ≤ 1 AND x > -1/7. This means we are looking for the intersection of the two solution sets.
The solution is the range of values for x that are greater than -1/7 and less than or equal to 1. We can express this as a compound inequality:
-1/7 < x ≤ 1
This represents the solution set for the original compound inequality.
Graphing the Solution
Visualizing the solution set on a number line can be very helpful. You would plot a hollow circle at -1/7 (because x is strictly greater than -1/7) and a filled circle at 1 (because x can be equal to 1). Then, you would shade the region between these two points. This shaded region represents all the values of x that satisfy the original inequality.
Checking the Solution
It's always a good practice to check your solution by plugging in values from within the solution set and values outside the solution set into the original inequality.
Example: Let's test x = 0 (which falls within the solution set -1/7 < x ≤ 1):
2 ≤ 4 - 2(0) < 5(0) + 5
2 ≤ 4 < 5
This is true, confirming that x = 0 is a valid solution.
Example: Let's test x = 2 (which falls outside the solution set):
2 ≤ 4 - 2(2) < 5(2) + 5
2 ≤ 0 < 15
This is false, confirming that x = 2 is not a valid solution.
Further Applications and Extensions
The principles used to solve this inequality can be extended to more complex compound inequalities involving polynomials, rational functions, or even absolute value expressions. The key is to break down the compound inequality into simpler inequalities, solve each one individually, and then find the intersection or union of the solution sets, depending on whether the inequality uses "and" or "or".
Remember to always pay close attention to the direction of the inequality signs and to reverse the sign when multiplying or dividing by a negative number. Careful attention to these details will ensure accurate and reliable solutions.
Common Mistakes to Avoid
-
Forgetting to reverse the inequality sign when multiplying or dividing by a negative number: This is a very common mistake that can lead to incorrect solutions. Always double-check this step.
-
Incorrectly combining the solution sets: Make sure you understand whether you need to find the intersection (using "and") or the union (using "or") of the solution sets.
-
Neglecting to check your solution: Always verify your solution by testing values within and outside the solution set in the original inequality.
Conclusion
Solving compound inequalities, such as 2 ≤ 4 - 2x < 5x + 5, involves a systematic approach of breaking the problem into simpler inequalities, solving each individually, and then carefully combining the results. Mastering this technique is essential for success in higher-level mathematics. By following the steps outlined in this article and paying attention to common pitfalls, you can confidently tackle similar problems and gain a deeper understanding of inequalities. Remember to always check your work to ensure the accuracy of your solutions. This comprehensive guide should equip you with the knowledge and confidence to successfully solve a wide range of compound inequalities.
Latest Posts
Related Post
Thank you for visiting our website which covers about Solve The Inequality 2 4 2x 5x 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.