Solve This Inequality 8z 3 2z 51
News Co
Apr 15, 2025 · 5 min read
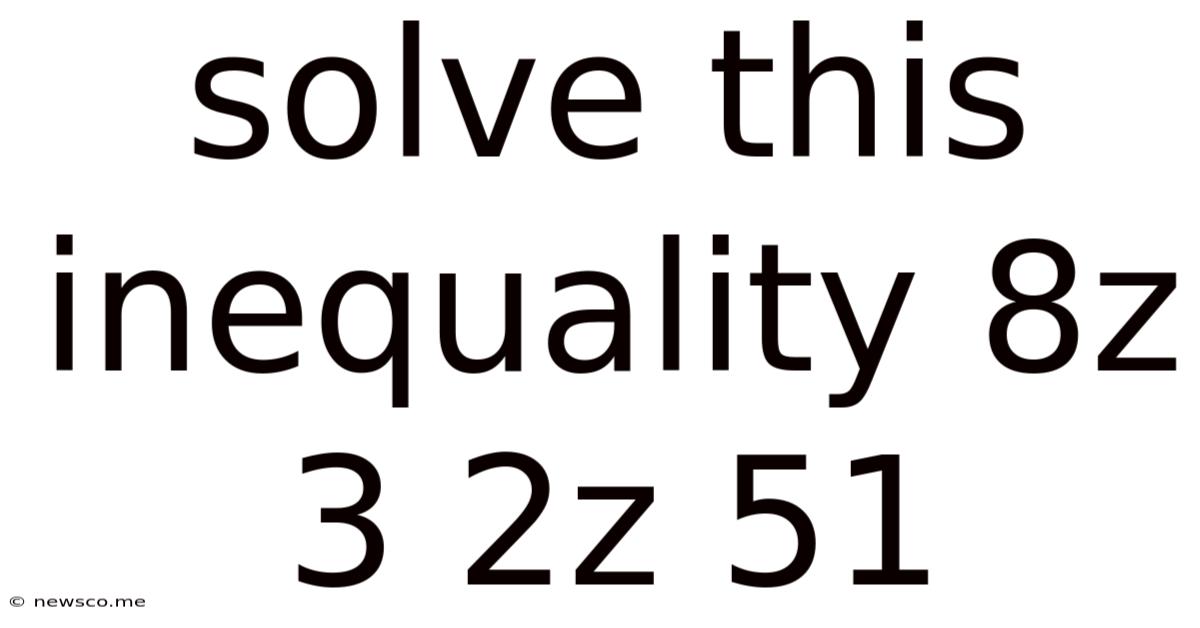
Table of Contents
Solving the Inequality: 8z + 3 ≥ 2z + 51
This article provides a comprehensive guide to solving the inequality 8z + 3 ≥ 2z + 51. We will explore the steps involved, explain the underlying concepts, and offer practical examples to solidify your understanding. We'll also delve into the broader context of solving inequalities, including different types of inequalities and how to represent solutions graphically. This in-depth approach aims to equip you with the skills to tackle similar problems confidently.
Understanding Inequalities
Before diving into the solution, let's establish a foundational understanding of inequalities. Unlike equations, which assert equality between two expressions, inequalities express a relationship of inequality. The symbols used are:
- ≥: Greater than or equal to
- ≤: Less than or equal to
- >: Greater than
- <: Less than
These symbols indicate that one expression is either greater than, less than, greater than or equal to, or less than or equal to another expression. Solving an inequality involves finding the range of values for the variable that satisfy the given inequality.
Step-by-Step Solution: 8z + 3 ≥ 2z + 51
Now, let's tackle the inequality 8z + 3 ≥ 2z + 51 step-by-step:
Step 1: Isolate the variable terms. Our goal is to get all terms containing the variable 'z' on one side of the inequality and all constant terms on the other side. To achieve this, we can subtract 2z from both sides:
8z + 3 - 2z ≥ 2z + 51 - 2z
This simplifies to:
6z + 3 ≥ 51
Step 2: Isolate the constant term. Next, we need to isolate the term with 'z'. We can subtract 3 from both sides:
6z + 3 - 3 ≥ 51 - 3
This simplifies to:
6z ≥ 48
Step 3: Solve for the variable. Finally, to solve for 'z', we divide both sides by 6. Crucially, when dividing or multiplying both sides of an inequality by a negative number, you must reverse the inequality sign. Since we're dividing by a positive number (6), we don't need to reverse the sign:
6z / 6 ≥ 48 / 6
This simplifies to:
z ≥ 8
Interpreting the Solution
The solution, z ≥ 8, means that any value of 'z' that is greater than or equal to 8 will satisfy the original inequality 8z + 3 ≥ 2z + 51. This includes 8, 8.1, 9, 10, 100, and so on. Any value less than 8 will not satisfy the inequality.
Graphical Representation
Inequalities can be represented graphically on a number line. For the inequality z ≥ 8, we would:
- Draw a number line.
- Mark the point 8 on the number line.
- Draw a closed circle (or a filled-in dot) at 8, indicating that 8 is included in the solution.
- Draw an arrow extending to the right from 8, indicating that all values greater than 8 are also part of the solution.
This visual representation helps to clearly illustrate the range of values that satisfy the inequality.
Types of Inequalities and Their Solutions
Understanding various types of inequalities is essential for mastering this concept. Let's explore some common types:
-
Linear Inequalities: These inequalities involve a variable raised to the power of 1. Our example, 8z + 3 ≥ 2z + 51, is a linear inequality. Solving linear inequalities typically involves manipulating the equation to isolate the variable.
-
Quadratic Inequalities: These inequalities involve a variable raised to the power of 2. Solving quadratic inequalities often requires factoring the quadratic expression and analyzing the sign of the expression in different intervals.
-
Polynomial Inequalities: These inequalities involve polynomials of degree higher than 2. Solving these requires techniques like finding roots and analyzing intervals.
-
Rational Inequalities: These inequalities involve rational expressions (fractions with variables in the numerator or denominator). Solving these often involves finding critical values where the expression is zero or undefined, and then analyzing the sign of the expression in intervals determined by these critical values.
-
Absolute Value Inequalities: These inequalities involve absolute value expressions. Solving these requires considering both the positive and negative cases of the absolute value expression.
Advanced Techniques and Considerations
Solving more complex inequalities might require advanced techniques:
-
Factoring: Factoring expressions is crucial for solving quadratic and polynomial inequalities. It allows you to find the roots (or zeros) of the expression, which are essential for determining the intervals where the inequality holds.
-
Interval Notation: Interval notation is a concise way to represent the solution set of an inequality. For our example, z ≥ 8, the interval notation is [8, ∞). The square bracket indicates that 8 is included, while the parenthesis indicates that infinity is not included.
-
Testing Intervals: After finding the roots of a polynomial or rational inequality, it's helpful to test values from each interval to determine whether the inequality holds true in that interval.
-
Graphing Calculators: For complex inequalities, graphing calculators or software can be used to visualize the solution set and verify your algebraic work. However, always understand the underlying algebraic principles to interpret the results correctly.
Real-World Applications of Inequalities
Inequalities are not just abstract mathematical concepts; they have numerous real-world applications:
-
Optimization Problems: Inequalities are frequently used to model optimization problems, where you seek to maximize or minimize a quantity subject to certain constraints. For instance, optimizing production costs or maximizing profit within budgetary constraints.
-
Engineering and Physics: Inequalities are essential in engineering and physics for modeling systems and constraints. For example, setting limits on stress or strain in structural design or defining stability criteria in control systems.
-
Economics: Economic models often use inequalities to represent budget constraints, production possibilities, or equilibrium conditions in markets.
-
Computer Science: Inequalities play a significant role in algorithm analysis, particularly in determining the time and space complexity of algorithms.
-
Finance: In financial modeling, inequalities can be used to express risk limits, return thresholds, or conditions for portfolio diversification.
Conclusion
Solving the inequality 8z + 3 ≥ 2z + 51 provides a foundation for understanding and solving a wide range of inequalities. Mastering this skill requires a solid grasp of algebraic manipulation, a clear understanding of inequality symbols, and the ability to interpret solutions graphically and within real-world contexts. By practicing with various types of inequalities and applying the techniques outlined in this article, you can develop confidence and proficiency in solving any inequality you encounter. Remember to always check your solutions by substituting values within the solution set back into the original inequality to confirm their validity. Practice is key to mastering this crucial mathematical skill.
Latest Posts
Related Post
Thank you for visiting our website which covers about Solve This Inequality 8z 3 2z 51 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.