Solve X 2 X 2 0
News Co
Apr 02, 2025 · 4 min read
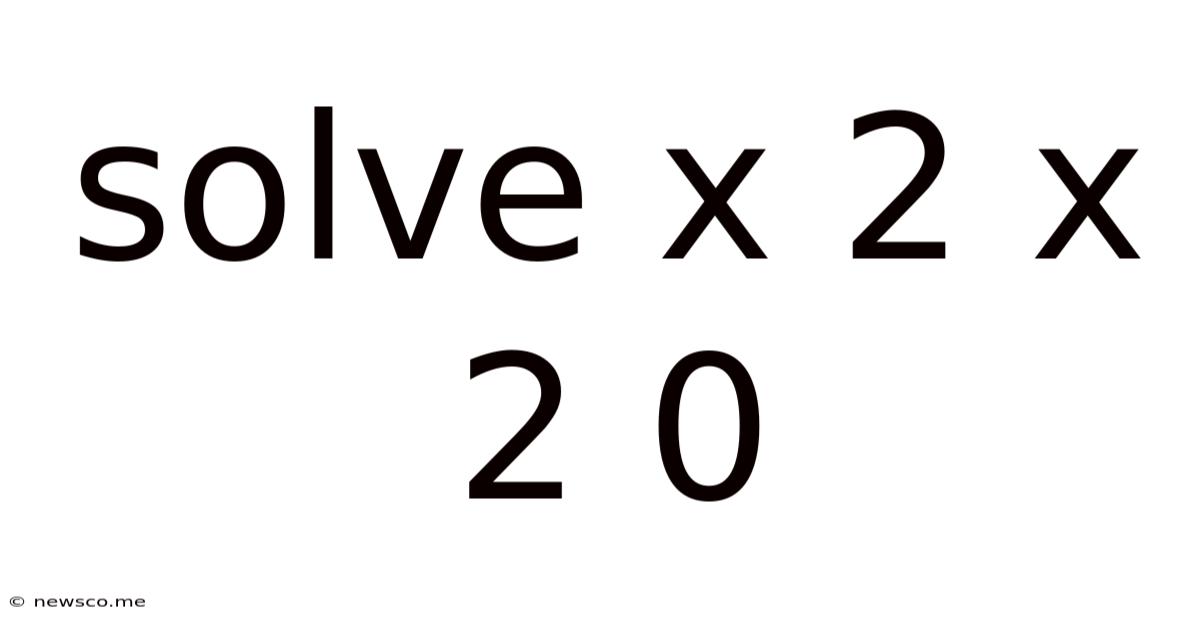
Table of Contents
Solving the Quadratic Equation: x² + 2x + 0 = 0
The equation x² + 2x + 0 = 0, while seemingly simple, provides a valuable opportunity to explore fundamental concepts in algebra, specifically quadratic equations and their solutions. Understanding how to solve this equation lays the groundwork for tackling more complex quadratic problems. This comprehensive guide will delve into various methods for solving this specific equation and provide a broader context for understanding quadratic equations in general.
Understanding Quadratic Equations
A quadratic equation is a polynomial equation of the second degree, meaning the highest power of the variable (in this case, 'x') is 2. The general form of a quadratic equation is:
ax² + bx + c = 0
where 'a', 'b', and 'c' are constants, and 'a' is not equal to zero (otherwise, it wouldn't be a quadratic equation). In our specific equation, x² + 2x + 0 = 0, we have:
- a = 1
- b = 2
- c = 0
This simplifies the equation considerably, making it easier to solve using several methods.
Method 1: Factoring
Factoring is a powerful technique for solving quadratic equations, especially when the equation is easily factorable. In this case, we can simplify the equation to:
x² + 2x = 0
Now, we can factor out an 'x':
x(x + 2) = 0
This equation is true if either of the factors equals zero. Therefore, we have two possible solutions:
- x = 0
- x + 2 = 0 => x = -2
Thus, the solutions to the equation x² + 2x + 0 = 0 are x = 0 and x = -2.
Method 2: Quadratic Formula
The quadratic formula is a more general method that can be used to solve any quadratic equation, regardless of its factorability. The formula is:
x = [-b ± √(b² - 4ac)] / 2a
Plugging in the values from our equation (a = 1, b = 2, c = 0), we get:
x = [-2 ± √(2² - 4 * 1 * 0)] / (2 * 1) x = [-2 ± √4] / 2 x = [-2 ± 2] / 2
This gives us two solutions:
- x = (-2 + 2) / 2 = 0
- x = (-2 - 2) / 2 = -2
Again, we arrive at the same solutions: x = 0 and x = -2. The quadratic formula provides a robust and universally applicable method for solving quadratic equations.
Method 3: Completing the Square
Completing the square is another algebraic technique for solving quadratic equations. This method involves manipulating the equation to create a perfect square trinomial, which can then be easily factored. Let's apply this to our equation:
x² + 2x = 0
To complete the square, we take half of the coefficient of the 'x' term (which is 2), square it (1), and add it to both sides of the equation:
x² + 2x + 1 = 1
Now, the left side is a perfect square trinomial:
(x + 1)² = 1
Taking the square root of both sides:
x + 1 = ±√1 x + 1 = ±1
This gives us two equations:
- x + 1 = 1 => x = 0
- x + 1 = -1 => x = -2
Once again, we obtain the solutions x = 0 and x = -2.
Graphical Representation
The solutions to a quadratic equation also represent the x-intercepts (where the graph crosses the x-axis) of the corresponding parabola. The equation x² + 2x + 0 = 0 represents a parabola that opens upwards. The x-intercepts are at x = 0 and x = -2, confirming our solutions. Visualizing the graph can provide a helpful understanding of the equation's behavior and its solutions.
Significance of the Solutions
The solutions x = 0 and x = -2 are the values of x that satisfy the given quadratic equation. These values represent the points where the parabola intersects the x-axis. In more complex applications, these solutions might represent critical points, such as the equilibrium points in a physical system or the break-even points in a business model.
Solving More Complex Quadratic Equations
The principles demonstrated here – factoring, the quadratic formula, and completing the square – are fundamental to solving more complex quadratic equations. While the equation x² + 2x + 0 = 0 provided a relatively straightforward illustration, applying these techniques to equations with non-zero 'c' values will require more steps but follow the same basic logic. Remember that the discriminant (b² - 4ac) within the quadratic formula determines the nature of the roots:
- b² - 4ac > 0: Two distinct real roots.
- b² - 4ac = 0: One real root (repeated root).
- b² - 4ac < 0: Two complex conjugate roots.
Applications of Quadratic Equations
Quadratic equations have wide-ranging applications across various fields, including:
- Physics: Calculating projectile motion, determining the trajectory of objects under the influence of gravity.
- Engineering: Designing structures, optimizing systems, and analyzing stresses.
- Economics: Modeling supply and demand, analyzing market trends.
- Computer Science: Developing algorithms and solving optimization problems.
Conclusion
Solving the seemingly simple quadratic equation x² + 2x + 0 = 0 offers a valuable entry point into the world of quadratic equations. By understanding the different methods for solving such equations – factoring, the quadratic formula, and completing the square – and appreciating their graphical representation, you build a strong foundation for tackling more complex problems. This understanding extends far beyond pure mathematics, finding practical application in diverse fields. Remember to practice applying these techniques regularly to master the art of solving quadratic equations and unlock their potential in various real-world scenarios. The seemingly simple problem presented here unlocks a world of mathematical and practical possibilities.
Latest Posts
Related Post
Thank you for visiting our website which covers about Solve X 2 X 2 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.