Solve X 3 2 X 3 2 0 Let U
News Co
Mar 25, 2025 · 5 min read
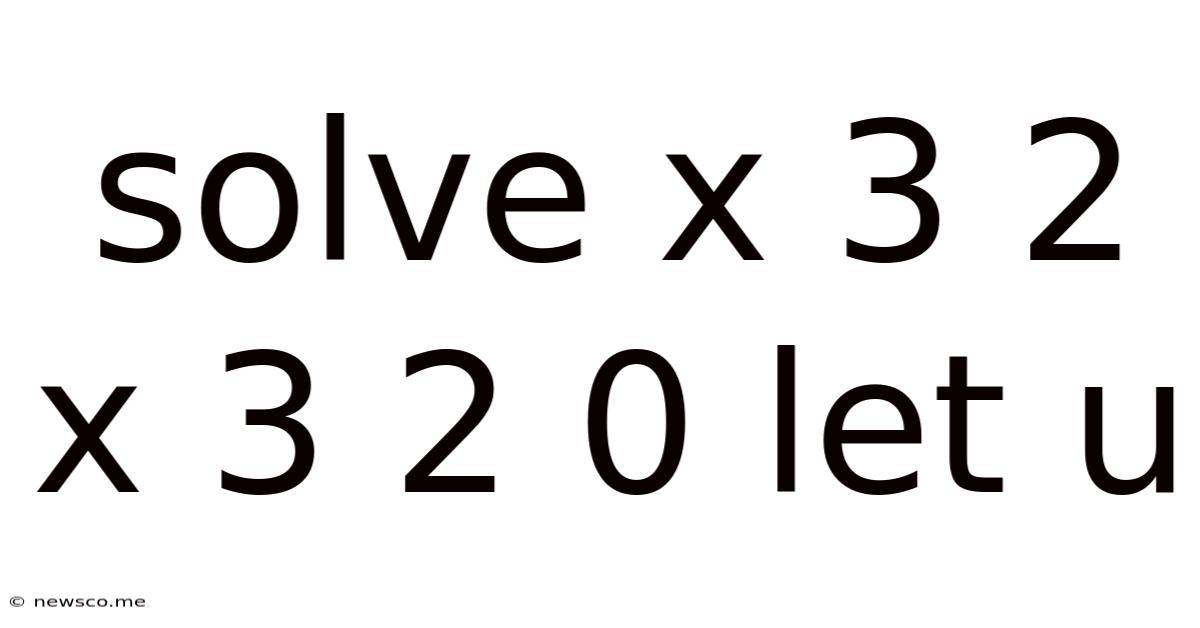
Table of Contents
Solving the Cubic Equation: x³ + 2x² - 3x - 2 = 0
This article delves into the solution of the cubic equation x³ + 2x² - 3x - 2 = 0, exploring various methods and providing a comprehensive understanding of the process. Cubic equations, unlike quadratic equations, don't always have readily apparent solutions, requiring more sophisticated techniques. We'll navigate through these techniques, illustrating the steps clearly and providing context for each method.
Understanding Cubic Equations
Before diving into the solution, let's understand the nature of cubic equations. A cubic equation is a polynomial equation of degree three, meaning the highest power of the variable (x in this case) is 3. The general form is ax³ + bx² + cx + d = 0, where a, b, c, and d are constants, and a ≠ 0. Our specific equation, x³ + 2x² - 3x - 2 = 0, has a = 1, b = 2, c = -3, and d = -2.
Cubic equations always have at least one real root (solution). They can have one real root and two complex conjugate roots, or three real roots (which may or may not be distinct). Determining the nature of the roots is part of the solution process.
Method 1: Rational Root Theorem and Polynomial Division
One approach to solving cubic equations is to utilize the Rational Root Theorem. This theorem states that if a polynomial equation with integer coefficients has a rational root p/q (where p and q are coprime integers), then p must be a factor of the constant term (d) and q must be a factor of the leading coefficient (a).
In our equation, x³ + 2x² - 3x - 2 = 0, the constant term is -2 and the leading coefficient is 1. Therefore, the possible rational roots are the factors of -2, which are ±1 and ±2.
Let's test these potential roots:
- x = 1: 1³ + 2(1)² - 3(1) - 2 = 1 + 2 - 3 - 2 = -2 ≠ 0
- x = -1: (-1)³ + 2(-1)² - 3(-1) - 2 = -1 + 2 + 3 - 2 = 2 ≠ 0
- x = 2: 2³ + 2(2)² - 3(2) - 2 = 8 + 8 - 6 - 2 = 8 ≠ 0
- x = -2: (-2)³ + 2(-2)² - 3(-2) - 2 = -8 + 8 + 6 - 2 = 4 ≠ 0
None of the potential rational roots work directly. However, this method might require further investigation using numerical methods or approximations.
Method 2: Numerical Methods (Iterative Techniques)
When analytical methods prove difficult, numerical methods provide approximate solutions. These methods use iterative processes to refine an initial guess until a sufficiently accurate solution is obtained. Examples include:
-
Newton-Raphson Method: This method uses the derivative of the function to iteratively improve the approximation of the root. The iterative formula is: x_(n+1) = x_n - f(x_n) / f'(x_n), where f(x) is the function and f'(x) is its derivative.
-
Bisection Method: This method repeatedly halves an interval known to contain a root, converging towards the root. It requires finding an interval where the function changes sign.
-
Secant Method: Similar to the Newton-Raphson method, but it approximates the derivative using the slope between two points on the function.
Applying these methods requires an initial guess and a tolerance for the desired accuracy. The calculations can be quite involved, often requiring computational tools or software.
Method 3: Substitution and Factoring (If Applicable)
Sometimes, a clever substitution can simplify the cubic equation, making it factorable. Unfortunately, there isn't an obvious substitution that simplifies our specific equation, x³ + 2x² - 3x - 2 = 0, readily. This method depends heavily on the specific form of the cubic equation.
Method 4: Cardano's Method (for General Cubic Equations)
Cardano's method is a general algebraic solution for cubic equations. It involves a series of substitutions and manipulations to arrive at the roots. However, the process is complex and prone to errors if not executed carefully. It's not the most practical approach for all cubic equations, especially those with easily identifiable roots or those amenable to simpler methods. The formula is quite lengthy and involves complex numbers even when dealing with only real roots.
Method 5: Graphical Method
Plotting the function y = x³ + 2x² - 3x - 2 allows for a visual identification of the roots. The x-intercepts of the graph represent the real roots of the equation. While this doesn't provide exact solutions, it offers a good approximation and insight into the nature of the roots (number of real roots).
Analyzing Our Specific Equation: x³ + 2x² - 3x - 2 = 0
Let's revisit our equation, x³ + 2x² - 3x - 2 = 0. Given the lack of readily apparent rational roots and the complexity of Cardano's method, numerical methods are likely the most practical approach for obtaining accurate solutions. A graphing calculator or software will reveal the approximate real roots.
Conclusion: A Multifaceted Approach to Cubic Equation Solving
Solving cubic equations is a multifaceted problem with various methods available. The best approach depends on the specific equation and the desired level of accuracy. While simple techniques like the rational root theorem are helpful in certain cases, more advanced methods such as numerical techniques or, in theory, Cardano's method, are often necessary for a complete solution. Understanding the characteristics of cubic equations and selecting the appropriate method are key steps in solving these complex polynomial equations effectively. The use of computational tools is frequently beneficial in simplifying the calculations involved, especially when dealing with numerical methods or Cardano's formula. Remember to always check your solutions by substituting them back into the original equation to verify their accuracy.
Latest Posts
Related Post
Thank you for visiting our website which covers about Solve X 3 2 X 3 2 0 Let U . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.